题目内容
已知函数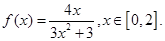
(1)求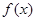 的值域;
的值域;
(2)设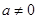 ,函数
,函数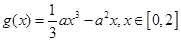 .若对任意
.若对任意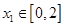 ,总存在
,总存在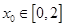 ,使
,使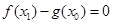 ,求实数
,求实数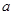 的取值范围.
的取值范围.
【答案】
(1) 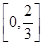 ;(2)
;(2) 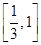
【解析】
试题分析:(1)求出 的导函数,令导函数等于求出
的导函数,令导函数等于求出 的值,然后由
的值,然后由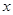 的值,分区间讨论导函数的正负得到函数的单调区间,根据函数的增减性得到函数的最大值和最小值即可得到
的值,分区间讨论导函数的正负得到函数的单调区间,根据函数的增减性得到函数的最大值和最小值即可得到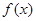 的值域;(2)设函数
的值域;(2)设函数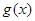 在[0,2]上的值域是A,根据题意对任意
在[0,2]上的值域是A,根据题意对任意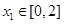 ,总存在
,总存在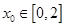 ,使
,使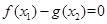 ,得到区间
,得到区间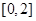 是A的子集,求出
是A的子集,求出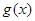 的导函数,分
的导函数,分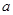 小于0和
小于0和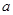 大于0两种情况讨论导函数的正负得到函数的单调区间,根据函数的增减性得到函数的最大值和最小值,即可得到函数在相应区间的值域,根据区间[0,2]是A的子集判断出符合这一条件的情况,列出关于
大于0两种情况讨论导函数的正负得到函数的单调区间,根据函数的增减性得到函数的最大值和最小值,即可得到函数在相应区间的值域,根据区间[0,2]是A的子集判断出符合这一条件的情况,列出关于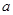 的不等式,求出不等式的解集即可得到满足题意
的不等式,求出不等式的解集即可得到满足题意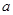 的取值范围.
的取值范围.
试题解析:(1)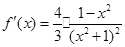 ,令
,令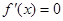 ,得
,得 或
或 .
.
当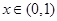 时,
时,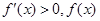 在
在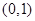 上单调递增;
上单调递增;
当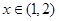 时,
时,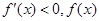 在
在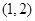 上单调递减,
上单调递减,
而 ,
,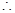 当
当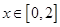 时,
时,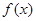 的值域是
的值域是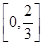 .
.
(2)设函数 在
在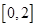 上的值域是A,
上的值域是A,
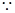 若对任意
若对任意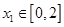 .总存在
.总存在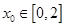 1,使
1,使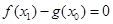 ,
,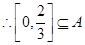 .
.
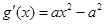 .
.
①当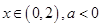 时,
时,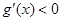 ,
, 函数
函数 在
在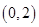 上单调递减.
上单调递减. 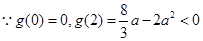 ,当
,当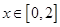 时,不满足
时,不满足 ;
;
②当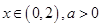 时,
时, ,令
,令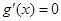 ,得
,得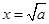 或
或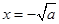 (舍去)
(舍去)
(i)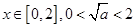 时,
时,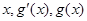 的变化如下表:
的变化如下表:
|
|
0 |
|
|
|
2 |
|
|
|
- |
0 |
+ |
|
|
|
0 |
|
|
|
|
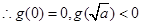 .
.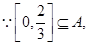
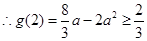 ,解得
,解得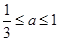 .
.
(ii)当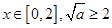 时,
时,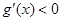 ,
,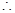 函数
函数 在
在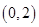 上单调递减.
上单调递减.
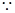
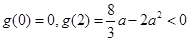 ,
,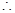 当
当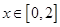 时,不满
时,不满 .
.
综上可知,实数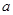 的取值范围是
的取值范围是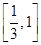 .
.
考点:1.函数的值域;2.导数求函数的单调性;3.分类讨论思想的运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
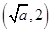
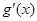

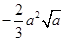
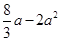
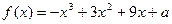
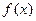 的单调递减区间;
的单调递减区间;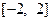 上的最大值为20, 求它在该区间上的最小值.
上的最大值为20, 求它在该区间上的最小值.
 .
.
 ,若对任意
,若对任意 ,均存在
,均存在 ,使得
,使得 ,求
,求
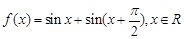 .
.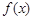 的最小正周期;
的最小正周期;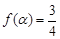 ,求
,求 的值.
的值.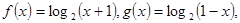
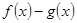 的定义域.
的定义域. 上的单调性并说明理由.
上的单调性并说明理由. .
. 的单调递增区间;
的单调递增区间;