题目内容
已知函数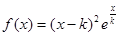 .
.
(1)求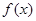 的单调区间;
的单调区间;
(2)若对于任意的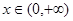 ,有
,有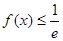 恒成立,求
恒成立,求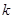 的取值范围.
的取值范围.
【答案】
(1)当k>0时,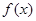 的单调递增区间是(
的单调递增区间是(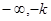 )和
)和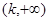 ;单调减区间是
;单调减区间是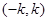 ;
;
当k<0时,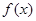 的单调递减区间是(
的单调递减区间是(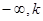 )和
)和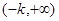 ;单调增区间是
;单调增区间是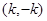
(2)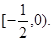
【解析】
试题分析:(1)由题意可得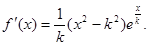
令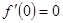 ,得
,得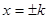 .
.
当k>0时,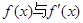 的情况如下
的情况如下
|
x |
( |
|
( |
k |
|
|
|
+ |
0 |
— |
0 |
+ |
|
|
↗ |
|
↘ |
0 |
↗ |
所以,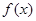 的单调递增区间是(
的单调递增区间是(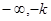 )和
)和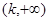 ;单调减区间是
;单调减区间是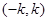 ;
;
当k<0时,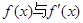 的情况如下
的情况如下
|
x |
( |
k |
(k, |
|
|
|
|
— |
0 |
+ |
0 |
— |
|
|
↘ |
0 |
↗ |
|
↘ |
所以,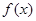 的单调递减区间是(
的单调递减区间是(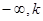 )和
)和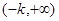 ;单调增区间是
;单调增区间是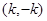
(2)当k>0时,因为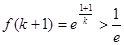 ,所以不会有
,所以不会有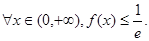
当k<0时,由(Ⅰ)知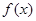 在(0,+
在(0,+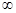 )上的最大值是
)上的最大值是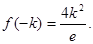
所以 等价于
等价于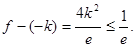
解得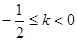 .
.
故当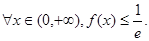 时,k的取值范围是
时,k的取值范围是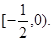
考点:本小题主要考查利用导数研究函数的性质和恒成立问题的求解.
点评:导数是研究函数性质的有力工具,研究函数时,首先要看函数的定义域,求单调区间、极值、最值时,往往离不开分类讨论,主要考查学生的分类讨论思想的应用和运算求解能力.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
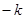
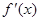
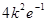
 .
. 的单调区间;
的单调区间; ,
, 在区间
在区间 恒成立,求a的取值范围.
恒成立,求a的取值范围. ,
,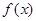 的单调递减区间;
的单调递减区间; 时,求函数
时,求函数 .
. .
. 的单调区间;
的单调区间; 时,判断
时,判断 和
和 的大小,并说明理由;
的大小,并说明理由; 时,关于
时,关于 的方程:
的方程: 在区间
在区间 上总有两个不同的解.
上总有两个不同的解. ,
,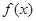 的最小值;
的最小值; 都有
都有 ,求实数
,求实数 的取值范围.
的取值范围.