Question

【题目】如图，在三棱柱中，侧面是矩形，，，，且.

（1）求证：平面平面；

（2）设是的中点，判断并证明在线段上是否存在点，使平面，若存在，求点到平面的距离.

Answer 1

【答案】(1)证明见解析；(2)为的中点，.

【解析】

试题分析：(1)借助题设条件运用面面垂直的判定定理推证；(2)借助题设运用线面平行的判定定理及等积法探求.

试题解析：

（1）在三棱柱中，侧面是矩形，

又，，

平面，

，又，，

又，，

平面，又平面，

平面平面………………………………………6分

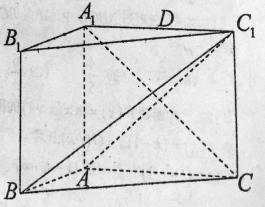
（2）解法一：当为的中点时，连接，

如图1，取的中点，连接，

，，

又，，

所以平面平面，又平面，

平面，

又因为，平面，

设点到平面的距离为，

，，

所以点到平面的距离为.…………………………………12分

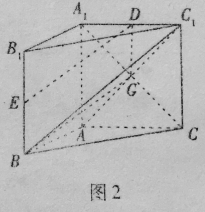
解法2.当为的中点时，连接，如图2，设交于点，连接，

且，

四边形为平行四边形，则，又平面，平面，

平面，

求距离同解法一.