题目内容
15．求y=$\frac{5}{2{x}^{2}-4x+3}$的值域．分析 利用配方法求出二次三项式2x2-4x+3的范围，取倒数后乘以5得答案．
解答 解：∵t=2x2-4x+3=$2（{x}^{2}-2x+\frac{3}{2}）$=2（x-1）2+1≥1，
∴$\frac{5}{2{x}^{2}-4x+3}$∈（0，5]，
即y=$\frac{5}{2{x}^{2}-4x+3}$的值域为（0，5]．
点评 本题考查函数值域的求法，训练了利用配方法求二次函数的值域，是基础题．
练习册系列答案
全能闯关100分系列答案
相关题目
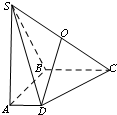如图，在四棱锥S-ABCD中，底面ABCD是直角梯形，AB⊥AD，AB⊥BC，侧棱SA⊥底面ABCD，点O为侧棱SC的中点，且SA=AB=BC=2，AD=1．
4．已知函数f（x）=4x2-kx-8在[1，4]上具有单调性，则实数k的取值范围是（ ）
| A． | （-∞，4]∪[16，+∞） | B． | [4，16] | C． | （-∞，8]∪[32，+∞） | D． | [8，32] |