Question

数列{a_n}中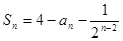，.（Ⅰ）求；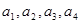

（Ⅱ）猜想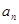的表达式，并用数学归纳法加以证明.

 

Answer 1

【答案】

解：（Ⅰ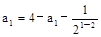）∵，∴，即a₁＝1，　

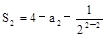∵，即a₁＋a₂＝4―a₂―1，∴a₂＝1，　　

　∵，即a₁＋a₂＋a₃＝4―a₃―，∴a₃＝，

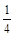∵，即a₁＋a₂＋a₃＋a₄＝4―a₄―，∴a₃＝，

（Ⅱ）猜想      

证明如下：①当n＝1时，a₁＝1，此时结论成立； 

②假设当n＝k（k∈N^*）结论成立，即，

那么当n＝k＋1时，有

 ,这就是说n＝k＋1时结论也成立.          

根据①和②，可知对任何n∈N^*时.      

【解析】略