题目内容
观察下列等式
1=1
2+3+4=9
3+4+5+6+7=25
4+5+6+7+8+9+10=49
…
照此规律,第n个等式为 _________ .
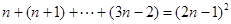
解析试题分析:根据题意,
第一个式子的左边是1,只有1个数,其中1=2×1-1,
第二个式子的左边是从2开始的3个数的和,其中3=2×2-1;
第三个式子的左边是从3开始的5个数的和,其中5=2×3-1;
第四个式子的左边是从4开始的7个数的和,其中7=2×4-1;
以此类推,第n个式子的左边是从n开始的(2n-1)个数的和,右边是求和的结果;
所以第n个等式为: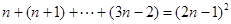 .
.
考点:归纳推理.

练习册系列答案
相关题目
下面是一段演绎推理:
如果直线平行于平面,则这条直线平行于平面内的所有直线;
已知直线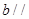 平面
平面 ,直线
,直线 平面
平面 ;
;
所以直线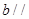 直线
直线 ,在这个推理中( )
,在这个推理中( )
| A.大前提正确,结论错误 |
| B.小前提与结论都是错误的 |
| C.大、小前提正确,只有结论错误 |
| D.大前提错误,结论错误 |
某人进行了如下的“三段论”推理:
如果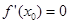 ,则
,则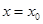 是函数
是函数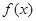 的极值点,因为函数
的极值点,因为函数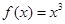 在
在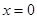 处的导数值
处的导数值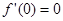 ,所以
,所以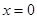 是函数
是函数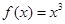 的极值点。你认为以上推理的
的极值点。你认为以上推理的
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.结论正确 |
用反证法证明命题“若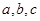 都是正数,则
都是正数,则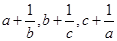 三数中至少有一个不小于
三数中至少有一个不小于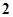 ”,提出的假设是( )
”,提出的假设是( )
A.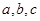 不全是正数 不全是正数 |
B.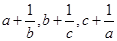 至少有一个小于 至少有一个小于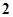 |
C.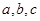 都是负数 都是负数 |
D.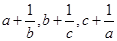 都小于2 都小于2 |
若大前提是:任何实数的平方都大于0,小前提是: ,结论是:
,结论是: ,那么这个演绎推理出错在:( )
,那么这个演绎推理出错在:( )
| A.大前提 | B.小前提 |
| C.推理过程 | D.没有出错 |
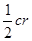 、
、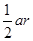 、
、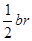 ,由
,由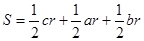 得
得 ,类比得四面体的体积为V,四个面的面积分别为
,类比得四面体的体积为V,四个面的面积分别为 ,则内切球的半径R=_________________
,则内切球的半径R=_________________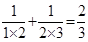 ,
,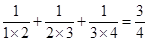 ,
, 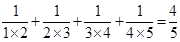 ,根据以上规律,写出第四个等式为:__________.
,根据以上规律,写出第四个等式为:__________.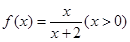 ,且
,且 当
当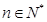 且
且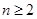 时,
时,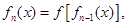 猜想
猜想 的表达式 .
的表达式 .