题目内容
已知边长分别为a、b、c的三角形ABC面积为S,内切圆O半径为r,连接OA、OB、OC,则三角形OAB、OBC、OAC的面积分别为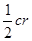 、
、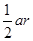 、
、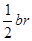 ,由
,由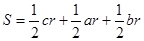 得
得 ,类比得四面体的体积为V,四个面的面积分别为
,类比得四面体的体积为V,四个面的面积分别为 ,则内切球的半径R=_________________
,则内切球的半径R=_________________
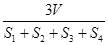
解析试题分析:设球心为O,分别连结四个顶点与球心O,将四面体分割成底面面积分别为 高为R的三棱锥,其体积分别为
高为R的三棱锥,其体积分别为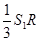 ,
,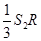 ,
,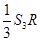 ,
,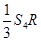 ,由V=
,由V=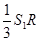 +
+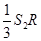 +
+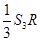 +
+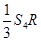 得,R=
得,R=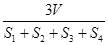 .
.
考点:类比推理

练习册系列答案
相关题目
下列三句话按三段论的模式排列顺序正确的是( )
① 2013不能被2整除; ② 一切奇数都不能被2整除; ③ 2013是奇数;
| A.①②③ | B.②①③ | C.②③① | D.③②① |
根据偶函数定义可推得“函数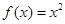 在
在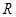 上是偶函数”的推理过程是( )
上是偶函数”的推理过程是( )
| A.归纳推理 | B.类比推理 | C.演绎推理 | D.非以上答案 |
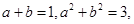
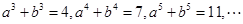 ,则依次类推可得
,则依次类推可得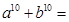 ;
;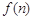 表示第
表示第 幅图的蜂巢总数,则
幅图的蜂巢总数,则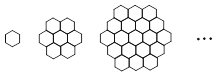
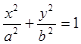 (
(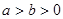 ),圆的标准方程
),圆的标准方程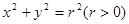 ,即
,即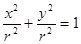 ,类比圆的面积
,类比圆的面积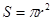 推理得椭圆的面积
推理得椭圆的面积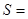 。
。
