题目内容
已知双曲线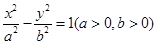 与抛物线
与抛物线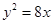 有一个公共的焦点
有一个公共的焦点 ,且两曲线的一个交点为
,且两曲线的一个交点为 ,若
,若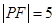 ,则双曲线的渐近线方程为.
,则双曲线的渐近线方程为.
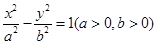 与抛物线
与抛物线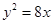 有一个公共的焦点
有一个公共的焦点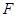 ,且两曲线的一个交点为
,且两曲线的一个交点为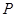 ,若
,若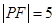 ,则双曲线的渐近线方程为.
,则双曲线的渐近线方程为.A. | B.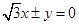 | C.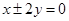 | D.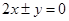 |
B
试题分析:抛物线
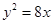 焦点
焦点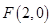 ,所以双曲线焦点为
,所以双曲线焦点为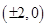
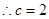 ,抛物线中
,抛物线中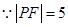 ,所以点P到准线
,所以点P到准线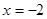 的距离为5,
的距离为5,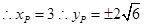 ,代入双曲线得
,代入双曲线得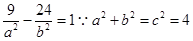
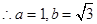 ,渐近线为
,渐近线为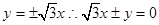
点评:本题的入手点在抛物线,首先由抛物线方程得到其性质,结合点P是两曲线的交点,通过点P将已知条件转换到双曲线中,进而求得双曲线方程

练习册系列答案
相关题目
 为椭圆
为椭圆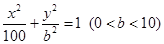 的左、右焦点,
的左、右焦点,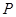 是椭圆上一点,若
是椭圆上一点,若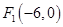 。
。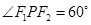 求
求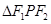 的面积。
的面积。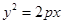 上,横坐标为
上,横坐标为 的点到焦点的距离为
的点到焦点的距离为 ,则
,则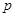 的值为( )
的值为( )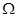 ,它的离心率为
,它的离心率为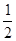 ,一个焦点和抛物线
,一个焦点和抛物线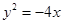 的焦点重合,过直线
的焦点重合,过直线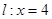 上一点
上一点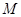 引椭圆
引椭圆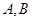 .
.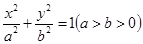 上的点
上的点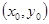 处的椭圆的切线方程是
处的椭圆的切线方程是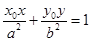 . 求证:直线
. 求证:直线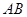 恒过定点
恒过定点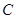 ;并出求定点
;并出求定点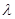 ,使得
,使得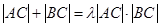 恒成立?(点
恒成立?(点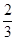 .
.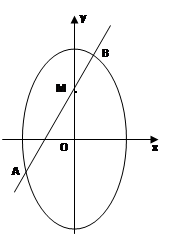
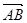 所成的比为2,求线段AB所在直线的方程.
所成的比为2,求线段AB所在直线的方程.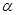 平行,P是直线
平行,P是直线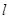 上的一点,平面
上的一点,平面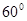 。那么B点轨迹是
。那么B点轨迹是 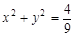 ,直线l:
,直线l: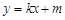 与椭圆C:
与椭圆C: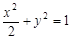 相交于P、Q两点,O为原点.
相交于P、Q两点,O为原点.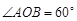 ,求直线l的方程;
,求直线l的方程;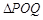 重心恰好在圆上,求m的取值范围.
重心恰好在圆上,求m的取值范围.
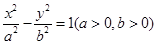 的右焦点
的右焦点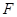 作圆
作圆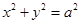 的切线
的切线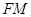 (切点为
(切点为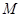 ),交
),交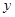 轴于点
轴于点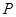 .若
.若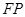 的中点,则双曲线的离心率为
的中点,则双曲线的离心率为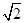
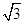
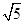
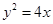 的焦点
的焦点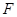 的直线交抛物线于
的直线交抛物线于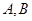 两点,满足
两点,满足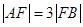 ,则弦
,则弦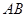 的中点到准线的距离为____.
的中点到准线的距离为____.