题目内容
11.已知函数f(x)=|x2-a|+|x-a|(a≥1),(1)当a=1时,试求函数f(x)单调区间,并求函数在[-2,2]上的最值;
(2)若f(x)=k有两个不相等的实数根,求实数k的取值范围.
分析 (1)化简f(x)=$\left\{\begin{array}{l}{{x}^{2}-x,x≤-1}\\{-{x}^{2}-x+2,-1<x<1}\\{{x}^{2}+x-2,x≥1}\end{array}\right.$,从而写出函数的单调区间及在[-2,2]上的最值即可;
(2)化简f(x)=$\left\{\begin{array}{l}{{x}^{2}-x,x≤-\sqrt{a}}\\{-{x}^{2}-x+2a,-\sqrt{a}<x<\sqrt{a}}\\{{x}^{2}-x,\sqrt{a}≤x≤a}\\{{x}^{2}+x-2a,x>a}\end{array}\right.$,从而确定函数的单调区间,作函数简图,由数形结合求实数k的取值范围.
解答 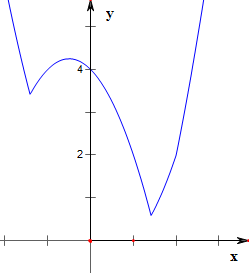 解:(1)当a=1时,
解:(1)当a=1时,
f(x)=|x2-1|+|x-1|=$\left\{\begin{array}{l}{{x}^{2}-x,x≤-1}\\{-{x}^{2}-x+2,-1<x<1}\\{{x}^{2}+x-2,x≥1}\end{array}\right.$,
由二次函数的性质可得,
f(x)的单调减区间为(-∞,-1],(-$\frac{1}{2}$,1),
f(x)的单调增区间为(-1,-$\frac{1}{2}$],[1,+∞);
在区间[-2,2]上,f(-2)=6,f(-$\frac{1}{2}$)=$\frac{9}{4}$,f(2)=4,f(1)=0;
故函数在[-2,2]上的最大值为6,最小值为0;
(2)函数f(x)=|x2-a|+|x-a|=$\left\{\begin{array}{l}{{x}^{2}-x,x≤-\sqrt{a}}\\{-{x}^{2}-x+2a,-\sqrt{a}<x<\sqrt{a}}\\{{x}^{2}-x,\sqrt{a}≤x≤a}\\{{x}^{2}+x-2a,x>a}\end{array}\right.$,
由二次函数的性质可得,
f(x)的单调减区间为(-∞,-$\sqrt{a}$],(-$\frac{1}{2}$,$\sqrt{a}$),
f(x)的单调增区间为(-$\sqrt{a}$,-$\frac{1}{2}$],[$\sqrt{a}$,+∞);
作函数f(x)=|x2-a|+|x-a|的简图如右图,
f(-$\sqrt{a}$)=a+$\sqrt{a}$,f(-$\frac{1}{2}$)=2a+$\frac{1}{4}$,f($\sqrt{a}$)=a-$\sqrt{a}$;
结合图象可得,
若f(x)=k有两个不相等的实数根,
则a-$\sqrt{a}$<k<a+$\sqrt{a}$或a+$\sqrt{a}$<k<2a+$\frac{1}{4}$.
故实数k的取值范围为(a-$\sqrt{a}$,a+$\sqrt{a}$)∪(a+$\sqrt{a}$,2a+$\frac{1}{4}$).
点评 本题考查了分段函数的应用及函数的性质的判断,同时考查了数形结合的思想应用,属于中档题.

 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案| A. | 2$\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{7}$ | D. | 4 |
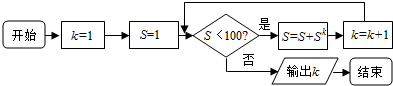
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |