题目内容
(2012•黄州区模拟)若不等式a+|
|≥2|log2x|在x∈(
,2)上恒成立,则实数a的取值范围为
| x2-1 |
| x |
| 1 |
| 2 |
a≥1
a≥1
.分析:先分离常数,然后构造函数,因为构造的函数中含有绝对值,所以要对给定的区间分段去掉绝对值变成分段函数,根据图象可求出最大值,这样就可以求出参数的取值范围.
解答: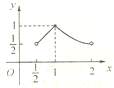 解:不等式即为a≥-|
解:不等式即为a≥-|
|+2|log2x|,在x∈(
,2)上恒成立.
而函数f(x)=-|
|+2|log2x|=
的图象如图所示,
所以f(x)在(
,2)上的最大值为1,所以a≥1.
故答案为:a≥1
 解:不等式即为a≥-|
解:不等式即为a≥-|| x2-1 |
| x |
| 1 |
| 2 |
而函数f(x)=-|
| x2-1 |
| x |
|
所以f(x)在(
| 1 |
| 2 |
故答案为:a≥1
点评:本题主要考查了函数恒成立问题,方法是分离常数之后构造函数,转化为函数求最值问题,本题中含绝对值,所以考虑先取绝对值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
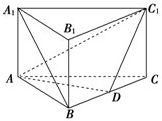 (2012•黄州区模拟)如图,在直三棱柱ABC-A1B1C1中,AB=BC=2AA1,∠ABC=90°,D是BC的中点.
(2012•黄州区模拟)如图,在直三棱柱ABC-A1B1C1中,AB=BC=2AA1,∠ABC=90°,D是BC的中点. (2012•黄州区模拟)已知某几何体的三视图如图,则该几何体的表面积为
(2012•黄州区模拟)已知某几何体的三视图如图,则该几何体的表面积为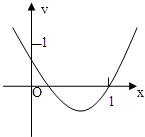 (2012•黄州区模拟)如图是二次函数f(x)=x2-bx+a的部分图象,则函数g(x)=2lnx+f(x)在点(b,g(b))处切线的斜率的最小值是( )
(2012•黄州区模拟)如图是二次函数f(x)=x2-bx+a的部分图象,则函数g(x)=2lnx+f(x)在点(b,g(b))处切线的斜率的最小值是( )