题目内容
已知函数 ,其中
,其中
(1)当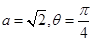 时,求
时,求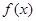 在区间
在区间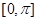 上的最大值与最小值;
上的最大值与最小值;
(2)若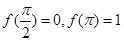 ,求
,求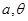 的值.
的值.
 ,其中
,其中
(1)当
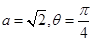 时,求
时,求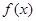 在区间
在区间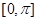 上的最大值与最小值;
上的最大值与最小值;(2)若
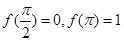 ,求
,求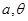 的值.
的值.(1)最大值为 最小值为-1. (2)
最小值为-1. (2)
 最小值为-1. (2)
最小值为-1. (2)
试题分析:(1)求三角函数最值,首先将其化为基本三角函数形式:当
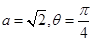 时,
时, ,再结合基本三角函数性质求最值:因为
,再结合基本三角函数性质求最值:因为 ,从而
,从而 ,故
,故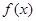 在
在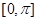 上的最大值为
上的最大值为 最小值为-1.(2)两个独立条件求两个未知数,联立方程组求解即可. 由
最小值为-1.(2)两个独立条件求两个未知数,联立方程组求解即可. 由 得
得 ,又
,又 知
知 解得
解得
试题解析:解(1)当
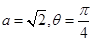 时,
时,
因为
 ,从而
,从而
故
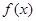 在
在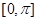 上的最大值为
上的最大值为 最小值为-1.
最小值为-1.(2)由
 得
得 ,又
,又 知
知 解得
解得

练习册系列答案
相关题目
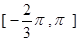 上的函数
上的函数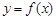 的图象关于直线
的图象关于直线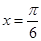 对称,当
对称,当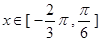 时函数
时函数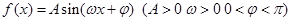 图象如图所示.
图象如图所示.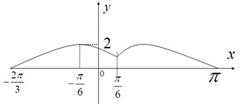
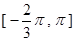 的表达式;
的表达式;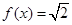 的解;
的解;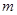 的值,使得
的值,使得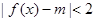 在
在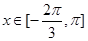 上恒成立;若存在,求出
上恒成立;若存在,求出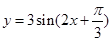 的图象向右平移
的图象向右平移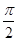 个单位长度,所得图象对应的函数( )
个单位长度,所得图象对应的函数( )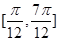 上单调递减
上单调递减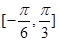 上单调递减
上单调递减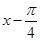 )= f(
)= f(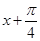 ),则下列函数中,符合上述条件的有_________.(填序号)
),则下列函数中,符合上述条件的有_________.(填序号)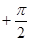 ) ③f(x)=sin(4x
) ③f(x)=sin(4x 4x)
4x) 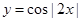 ,②
,②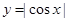 ,③
,③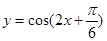 ,④
,④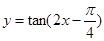 中,最小正周期为
中,最小正周期为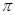 的所有函数为
的所有函数为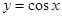 与函数
与函数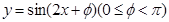 ,它们的图像有一个横坐标为
,它们的图像有一个横坐标为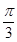 的交点,则
的交点,则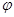 的值是 .
的值是 .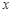 方程
方程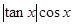 =a在区间
=a在区间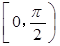
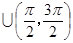 上有两个不同的实根,则实数a的取值范围为__________________.
上有两个不同的实根,则实数a的取值范围为__________________.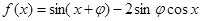 的最大值为________.
的最大值为________.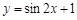 的最小正周期为 .
的最小正周期为 .