题目内容
17．已知两点A（-3，4），B（3，2），过点C（2，-1）的直线l与线段AB有公共点，则直线l的斜率k的取值范围（ ）| A． | k≤-3或k≥1 | B． | k≤-1或k≥3 | C． | -3≤k≤1 | D． | -1≤k≤3 |
分析 根据题意，画出图形，结合图形，求出满足条件的直线l斜率k的取值范围．
解答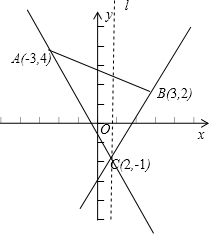 
解：如图所示，
∵A（-3，4），B（3，2），C（2，-1），
∴kAC=$\frac{-1-4}{2+3}$=-1，
kBC=$\frac{-1-2}{2-3}$=3；
要使过点C的直线l与线段AB有公共点，
则直线l的斜率k的取值范围是k≤-1或k≥3．
故选：B．
点评 本题考查了已知两点的坐标求直线斜率的应用问题，也考查了数形结合的应用问题，是基础题目．
练习册系列答案
相关题目
12．下列数列中为递增数列的是（ ）
| A． | {sinnπ} | B． | {n2-9n+5} | C． | {$\frac{2n+1}{{n}^{2}}$} | D． | {$\frac{{n}^{2}}{{n}^{2}+1}$} |