题目内容
1．已知集合M={（a，b）|a≤-1，且 0＜b≤m}，其中m∈R．若任意（a，b）∈M，均有alog2b-b-3a≥0，求实数m的最大值2．分析 如图所示，由alog2b-b-3a≥0，化为：$lo{g}_{2}b≤\frac{b}{a}+3$．由于$\frac{b}{a}$≥-m，b≤m时，可得log2m≤3-m．结合图形即可得出．
解答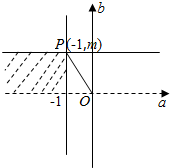 
解：如图所示，由alog2b-b-3a≥0，化为：$lo{g}_{2}b≤\frac{b}{a}+3$．
∵$\frac{b}{a}$≥-m，b≤m时，
∴log2m≤3-m．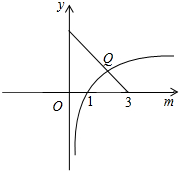
当m=2时取等号，
∴实数m的最大值为2．
点评 本题考查了函数的单调性、斜率，考查了数形结合思想方法、推理能力与计算能力，属于中档题．
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
12．复数z1=1+2i，z2=1-i，则z=$\frac{{z}_{1}•{z}_{2}}{1+i}$在复平面内的对应点位于（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
16．将函数f（x）=sin4x+$\sqrt{3}$cos4x的图象上每个点的横坐标变为原来的4倍（纵坐标不变），再将所得的图象向左平移φ个单位后的图象所对应的函数恰为偶函数，则φ的值可以是（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{12}$ | C． | $\frac{5π}{6}$ | D． | $\frac{π}{24}$ |
13．已知集合A={x|（x-1）2＜3x+7，x∈R}，B=$\left\{{x\left|{\frac{x}{x+1}≤0}\right.}\right\}$，则A∩B=（ ）
| A． | [-1，0] | B． | （-1，0） | C． | （-1，0] | D． | [-1，0） |