题目内容
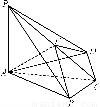
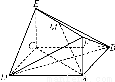
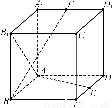
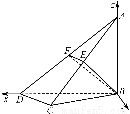
如图甲,在平面四边形ABCD中,已知∠A=45°,∠C=90°,∠ADC=105°,AB=BD,现将四边形ABCD沿BD折起,使平面ABD⊥平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.
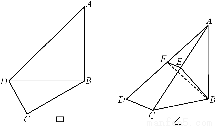
(1)求证:DC⊥平面ABC;
(2)求BF与平面ABC所成角的正弦值;
(3)求二面角B-EF-A的余弦值.
(1)见解析(2)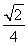 (3)-
(3)-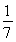
【解析】(1)∵平面ABD⊥平面BDC,又∵AB⊥BD,∴AB⊥平面BDC,故AB⊥DC,又∵∠C=90°,∴DC⊥BC,BC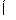 ?ABC平面ABC,DC
?ABC平面ABC,DC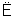 平面ABC,故DC⊥平面ABC.
平面ABC,故DC⊥平面ABC.
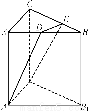
(2)如图,以B为坐标原点,BD所在的直线为x轴建立空间直角坐标系如下图示,设CD=a,则BD=AB=2a,BC=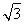 a,AD=2
a,AD=2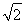 a,可得B(0,0,0),D(2a,0,0),A(0,0,2a),C
a,可得B(0,0,0),D(2a,0,0),A(0,0,2a),C ,F(a,0,a),
,F(a,0,a),
∴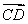 =
= ,
,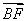 =(a,0,a).
=(a,0,a).
设BF与平面ABC所成的角为θ,由(1)知DC⊥平面ABC,
∴cos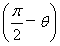 =
=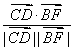 =
= =
=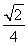 ,∴sinθ=
,∴sinθ=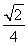 .
.
(3)由(2)知FE⊥平面ABC,又∵BE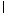 平面ABC,AE
平面ABC,AE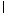 平面ABC,∴FE⊥BE,FE⊥AE,
平面ABC,∴FE⊥BE,FE⊥AE,
∴∠AEB为二面角B-EF-A的平面角.
在△AEB中,AE=BE=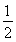 AC=
AC=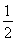
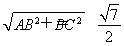 a,
a,
∴cos∠AEB=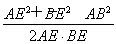 =-
=-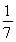 ,即所求二面角B-EF-A的余弦为-
,即所求二面角B-EF-A的余弦为-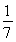 .
.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目