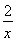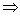题目内容
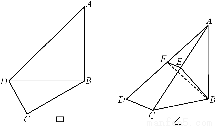
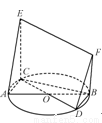
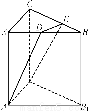
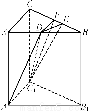
如图，底面边长为a，高为h的正三棱柱ABC-A1B1C1，其中D是AB的中点，E是BC的三等分点．求几何体BDEA1B1C1的体积．
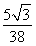a2h.
【解析】学生错【解析】
解∵BD＝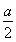
，BE＝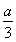
，∠DBE＝60°，
∴S△DBE＝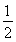
BD·BEsin∠DBE＝
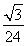a2，S△A1B1C1＝
·A1B1·B1C1sin60°＝
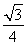a2.
由棱台体积公式得
VBDEA1B1C1＝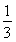
h(S△BDE＋S△A1B1C1＋
)
＝
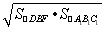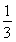h
＝
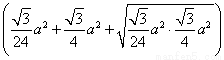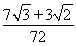a2h.
审题引导：(1)弄清组合体的结构，这里几何体DBEA1B1C1不是棱台，也可补上一个三棱锥使之成为一个三棱台；(2)运用体积公式进行计算．
规范解答：
【解析】
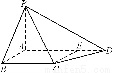
如图，取BC中点F，连结DF、C1D、C1E、C1F，得正三棱台DBFA1B1C1及三棱锥C1DEF.
∵S△A1B1C1＝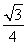
a2，S△DBF＝
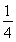S△ABC＝
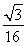a2，(4分)
∴VDBFA1B1C1＝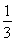
h(S△DBF＋S△A1B1C1＋)
＝
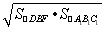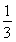h(
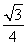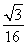a2＋
a2＋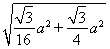
)＝
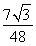a2h.(8分)
∴VC1DEF＝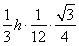
a2＝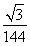
a2h，(10分)
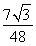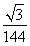∴VBDEA1B1C1＝VDBFA1B1C1VC1DEF＝a2h－
a2h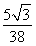＝a2h.(14分)
错因分析：没有弄清所给几何体的结构，几何体DBEA1B1C1不是棱台．
练习册系列答案
相关题目
