Question

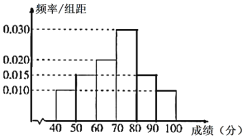
【题目】某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名学生的课外体育锻炼平均每天运动的时间(单位:min)进行调查,将收集到的数据分成[0,10),[10,20),[20,30),[30,40),[40,50),[50,60]六组,并作出频率分布直方图(如图).将日均课外体育锻炼时间不低于40 min的学生评价为“课外体育达标”.

(1)请根据频率分布直方图中的数据填写下面的2×2列联表,并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“课外体育达标”与性别有关?

	课外体育不达标	课外体育达标	总计
男	60
女			110
总计

(2)现从“课外体育达标”学生中按分层抽样抽取5人,再从这5名学生中随机抽取2人参加体育知识问卷调查,求抽取的这2人课外体育锻炼时间都在[40,50)内的概率.

附参考公式与数据:K2=

P(K2≥k0)	0.10	0.05	0.010	0.005	0.001
k0	2.706	3.841	6.635	7.879	10.828

Answer 1

【答案】(1)答案见解析；(2)0.6.

【解析】试题分析：

(1)根据频率分布直方图,得“课外体育达标”的学生数为50.由2×2列联表可知“课外体育达标”的男生人数为30,女生人数为20.据此完成列联表即可，计算观测值K2≈6.061<6.635,故在犯错误的概率不超过0.01的前提下不能认为“课外体育达标”与性别有关.

(2)从“课外体育达标”学生中按分层抽样抽取5人,其中课外体育锻炼时间在[40,50)内有4人,列出所有可能的基本事件，共有10种,其中2人都在[40,50)内的基本事件有6种,故所求的概率为=0.6.

试题解析：

(1)根据频率分布直方图,得“课外体育达标”的学生数为200×(0.020+0.005)×10=50.

由2×2列联表可知“课外体育达标”的男生人数为30,女生人数为20.

补全2×2列联表如下:

	课外体育不达标	课外体育达标	总计
男	60	30	90
女	90	20	110
总计	150	50	200

计算K2=≈6.061<6.635,故在犯错误的概率不超过0.01的前提下不能认为“课外体育达标”与性别有关.

(2)从“课外体育达标”学生中按分层抽样抽取5人,其中课外体育锻炼时间在[40,50)内有5×=4(人),分别记为a,b,c,d;

在[50,60]上有1人,记为E.

从这5人中抽取2人,总的基本事件有ab,ac,ad,aE,bc,bd,bE,cd,cE,dE共10种,其中2人都在[40,50)内的基本事件有ab,ac,ad,bc,bd,cd共6种,故所求的概率为=0.6.