题目内容
【题目】已知f(x)是定义在[-1,1]上的奇函数,且f(1)=1,若任意的a、b∈[-1,1],当a+b≠0时,总有![]() .
.
(1)判断函数f(x)在[-1,1]上的单调性,并证明你的结论;
(2)解不等式:![]() ;
;
(3)若f(x)≤m2-2pm+1对所有的x∈[-1,1]恒成立,其中p∈[-1,1](p是常数),试用常数p表示实数m的取值范围.
【答案】(1)![]() 在
在![]() 上是增函数,证明如下:
上是增函数,证明如下:
任取![]() ,且
,且![]() ,则
,则![]() ,于是有
,于是有![]() ,而
,而![]() ,故
,故![]() ,故
,故![]() 在
在![]() 上是增函数
上是增函数
(2)![]() .
.
(3)由(1)知![]() 最大值为
最大值为![]() ,所以要使
,所以要使![]() 对所有的
对所有的![]() 恒成立,只需
恒成立,只需![]() 成立,即
成立,即![]() 成立.
成立.
①当![]() 时,
时,![]() 的取值范围为
的取值范围为![]() ;
;
②当![]() 时,
时,![]() 的取值范围为
的取值范围为![]() ;
;
③当![]() 时,
时,![]() 的取值范围为R.
的取值范围为R.
【解析】
(1)![]() 在
在![]() 上是增函数,证明如下:
上是增函数,证明如下:
任取![]() ,且
,且![]() ,则
,则![]() ,于是有
,于是有![]() ,而
,而![]() ,故
,故![]() ,故
,故![]() 在
在![]() 上是增函数
上是增函数
(2)由![]() 在
在![]() 上是增函数知:
上是增函数知:
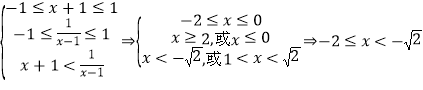 ,
,
故不等式的解集为![]() .
.
(3)由(1)知![]() 最大值为
最大值为![]() ,所以要使
,所以要使![]() 对所有的
对所有的![]() 恒成立,只需
恒成立,只需![]() 成立,即
成立,即![]() 成立.
成立.
①当![]() 时,
时,![]() 的取值范围为
的取值范围为![]() ;
;
②当![]() 时,
时,![]() 的取值范围为
的取值范围为![]() ;
;
③当![]() 时,
时,![]() 的取值范围为R.
的取值范围为R.

练习册系列答案
相关题目