题目内容
已知x,y均为正数,且x≠y,则下列四个数中最大的一个是( )
(A) (
(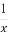 +
+ ) (B)
) (B)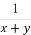
(C)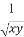 (D)
(D)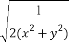
A
【解析】取x=1,y=2,可得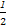 (
(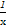 +
+ )=
)=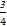 ,
,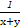 =
=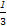 ,
,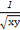 =
=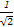 ,
,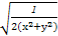 =
=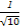 ,因此最大的是
,因此最大的是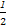 (
(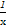 +
+ ),故选A.
),故选A.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
题目内容
已知x,y均为正数,且x≠y,则下列四个数中最大的一个是( )
(A) (
(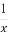 +
+ ) (B)
) (B)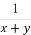
(C)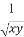 (D)
(D)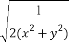
A
【解析】取x=1,y=2,可得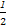 (
(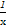 +
+ )=
)=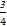 ,
,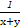 =
=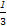 ,
,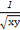 =
=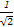 ,
,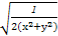 =
=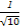 ,因此最大的是
,因此最大的是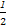 (
(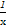 +
+ ),故选A.
),故选A.

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案