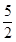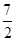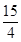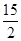题目内容
解关于x的不等式(1-ax)2<1.
当a<0时,原不等式解集为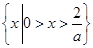 ;当a>0时,原不等式解集为
;当a>0时,原不等式解集为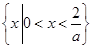
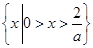 ;当a>0时,原不等式解集为
;当a>0时,原不等式解集为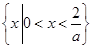
由(1-ax)2<1得a2x2-2ax+1<1,即ax(ax-2)<0.
①当a=0时,不等式转化为0<0,故x无解.
②当a<0时,不等式转化为x(ax-2)>0,即x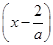 <0.
<0.
∵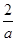 <0,∴不等式的解集为
<0,∴不等式的解集为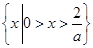 .
.
③当a>0时,原不等式转化为x(ax-2)<0,又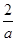 >0,即原不等式的解集为
>0,即原不等式的解集为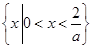 .
.
综上所述,当a=0时,原不等式解集为?;
当a<0时,原不等式解集为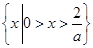 ;当a>0时,原不等式解集为
;当a>0时,原不等式解集为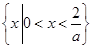 .
.
①当a=0时,不等式转化为0<0,故x无解.
②当a<0时,不等式转化为x(ax-2)>0,即x
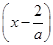 <0.
<0.∵
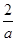 <0,∴不等式的解集为
<0,∴不等式的解集为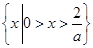 .
.③当a>0时,原不等式转化为x(ax-2)<0,又
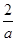 >0,即原不等式的解集为
>0,即原不等式的解集为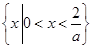 .
.综上所述,当a=0时,原不等式解集为?;
当a<0时,原不等式解集为
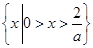 ;当a>0时,原不等式解集为
;当a>0时,原不等式解集为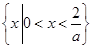 .
.
练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
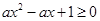 恒成立,则实数a的取值范围为 ________;
恒成立,则实数a的取值范围为 ________; 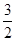 ,+∞),f(
,+∞),f(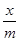 )-4m2f(x)≤f(x-1)+4f(m)恒成立,则实数m的取值范围是________.
)-4m2f(x)≤f(x-1)+4f(m)恒成立,则实数m的取值范围是________.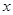 的不等式
的不等式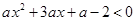 的解集为
的解集为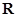 ,则实数
,则实数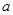 的取值范围 .
的取值范围 .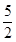
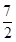
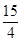
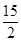
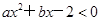 的解集为
的解集为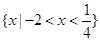 ,则
,则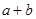 等于 .
等于 .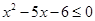 的解集为____________.
的解集为____________.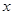 的不等式
的不等式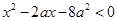 (
(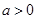 )的解集为
)的解集为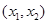 ,且
,且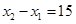 ,则
,则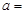 ( )
( )