题目内容
3．
如图，飞船返回舱顺利到达地球后，为了及时将航天员救出，地面指挥中心在返回舱预计到达区域安排了三个救援中心（记为A，B，C），B在A的正东方向，相距6km，C在B的北偏东30°的方向上，相距4km，P为航天员着陆点．某一时刻，在A地接到P的求救信号，由于B，C两地比A距P远，因此4s后，B，C两个救援中心才同时接收到这一信号，已知该信号的传播速度为1km/s．求∠BAP的大小．
分析 以AB中点为坐标原点，AB所在直线为x轴建立平面直角坐标系，易判断P在以A，B为焦点的双曲线的左支上，从而可确定双曲线的方程，再与BC的垂直平分线的方程联立，可求P的坐标，从而问题得解．
解答 解：以AB中点为坐标原点，AB所在直线为x轴建立平面直角坐标系，…（2分）
因为|PC|=|PB|，所以P在线段BC的垂直平分线上．
又因为|PB|-|PA|=4，|AB|=6，
所以P在以A，B为焦点的双曲线$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{5}=1$的左支上．…（6分）
又BC的垂直平分线方程为x+$\sqrt{3}$y-7=0…（8分）
联立两方程解得x=-8．
所以P（-8，5$\sqrt{3}$）…（10分）
所以kPA=tan∠PAB=-$\sqrt{3}$，得∠PAB=120°．…（12分）
点评 本题主要考查了解三角形的实际应用．解此类题的要点是建立适当的三角函数模型，利用三角函数的基本公式和定理进行求解．
练习册系列答案
步步高口算题卡系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案
相关题目
13．若a＜b＜0，则下列结论一定正确的是（ ）
| A． | $\frac{a+b}{2}$＞$\sqrt{ab}$ | B． | $\frac{1}{|a|}$＞$\frac{1}{|b|}$ | C． | ac2＜bc2 | D． | （a+$\frac{1}{b}$）2＞（b+$\frac{1}{a}$）2 |
18．
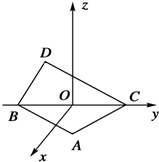如图所示，在空间直角坐标系中BC=2，原点O是BC的中点，点A的坐标是（$\frac{\sqrt{3}}{2}$，$\frac{1}{2}$，0），点D在平面yOz上，且∠BDC=90°，∠DCB=30°，则向量$\overrightarrow{AD}$的坐标为（ ）
如图所示，在空间直角坐标系中BC=2，原点O是BC的中点，点A的坐标是（$\frac{\sqrt{3}}{2}$，$\frac{1}{2}$，0），点D在平面yOz上，且∠BDC=90°，∠DCB=30°，则向量$\overrightarrow{AD}$的坐标为（ ）| A． | （-$\frac{\sqrt{3}}{2}$，-$\frac{1}{2}$，$\frac{\sqrt{3}}{2}$） | B． | （-$\frac{\sqrt{3}}{2}$，-1，$\frac{\sqrt{3}}{2}$） | C． | （-$\frac{1}{2}$，-$\frac{\sqrt{3}}{2}$，$\frac{\sqrt{3}}{2}$） | D． | （$\frac{\sqrt{3}}{2}$，1，$\frac{\sqrt{3}}{2}$） |
15．下列函数中，周期为π的是（ ）
| A． | y=cos4x | B． | y=tan2x | C． | y=sin2x | D． | $y=sin\frac{x}{2}$ |
12．命题：?x∈R，x＞0的否定为（ ）
| A． | ?x∈R，x≤0 | B． | ?x0∈R，x0＞0 | C． | ?x0∈R，x0≤0 | D． | ?x∈R，x＜0 |