题目内容
如果函数 满足在集合
满足在集合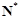 上的值域仍是集合
上的值域仍是集合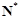 ,则把函数
,则把函数 称为N函数.
称为N函数.
例如: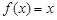 就是N函数.
就是N函数.
(Ⅰ)判断下列函数:①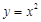 ,②
,②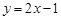 ,③
,③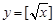 中,哪些是N函数?(只需写出判断结果);
中,哪些是N函数?(只需写出判断结果);
(Ⅱ)判断函数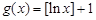 是否为N函数,并证明你的结论;
是否为N函数,并证明你的结论;
(Ⅲ)证明:对于任意实数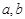 ,函数
,函数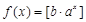 都不是N函数.
都不是N函数.
(注:“ ”表示不超过
”表示不超过 的最大整数)
的最大整数)
(Ⅰ)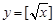 ;(Ⅱ)是N函数;(Ⅲ)略
;(Ⅱ)是N函数;(Ⅲ)略
解析试题分析:(Ⅰ)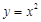 的定义域为
的定义域为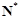 时,值域不是集合
时,值域不是集合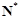 ,例如值域中不含2。故
,例如值域中不含2。故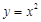 不是N函数 。
不是N函数 。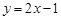 的定义域为
的定义域为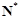 时,值域不是集合
时,值域不是集合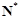 ,例如值域中不含2。故
,例如值域中不含2。故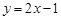 不是N函数。当
不是N函数。当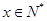 时
时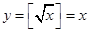 ,所以
,所以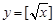 是N函数。(Ⅱ)因为“
是N函数。(Ⅱ)因为“ ”表示不超过
”表示不超过 的最大整数,所以
的最大整数,所以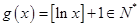 。设
。设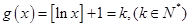 ,则
,则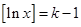 ,所以
,所以 ,解得
,解得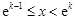 ,因为
,因为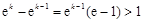 所以在
所以在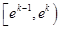 一定存在正整数
一定存在正整数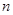 ,即存在
,即存在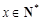 满足
满足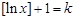 (Ⅲ)需对实数
(Ⅲ)需对实数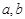 在全体实数范围内进行讨论。若
在全体实数范围内进行讨论。若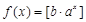 为负时,函数
为负时,函数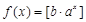 不是N函数;若函数
不是N函数;若函数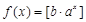 有最大值时,函数
有最大值时,函数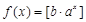 不是N函数;若函数
不是N函数;若函数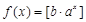 的值是正数但不能取到所有正数时,函数
的值是正数但不能取到所有正数时,函数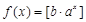 不是N函数。
不是N函数。
试题解析:解:(Ⅰ)只有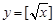 是N函数. 3分
是N函数. 3分
(Ⅱ)函数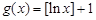 是N函数.
是N函数.
证明如下:
显然,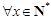 ,
,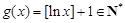 . 4分
. 4分
不妨设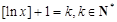 ,
,
由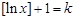 可得
可得 ,
,
即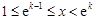 .
.
因为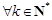 ,恒有
,恒有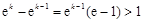 成立,
成立,
所以一定存在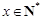 ,满足
,满足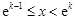 ,
,
所以设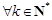 ,总存在
,总存在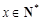 满足
满足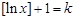 ,
,
所以函数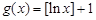 是N函数. 8分
是N函数. 8分
(Ⅲ)(1)当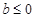 时,有
时,有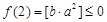 ,
,
所以函数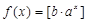 都不是N函数. 9分
都不是N函数. 9分
(2)当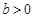 时,① 若
时,① 若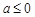 ,有
,有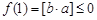 ,
,
所以函数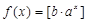 都不是N函数. 10分
都不是N函数. 10分
② 若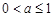 ,由指数函数性质易得
,由指数函数性质易得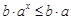 ,
,
所以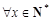 ,都有
,都有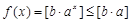
所以函数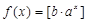 都不是N函数. 11分
都不是N函数. 11分
③ 若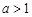 ,令
,令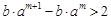 ,则
,则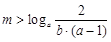 ,
,
所以一定存在正整数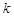 使得
使得 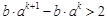 ,
,
所以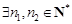 ,使得
,使得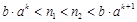 ,
,
所以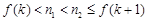 .
.
又因为当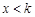 时,
时,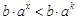 ,所以
,所以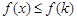 ;
;
当
练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
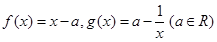 .
. 在
在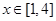 的单调性并用定义证明;
的单调性并用定义证明;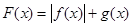 ,求
,求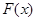 在区间
在区间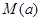 .
. .
. 有两个零点,求
有两个零点,求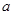 的取值范围;
的取值范围; 与
与 上各有一个零点,求
上各有一个零点,求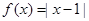
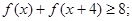
 .求证:
.求证: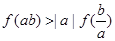 .
.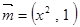 ,
,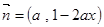 ,其中
,其中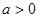 .函数
.函数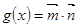 在区间
在区间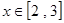 上有最大值为4,设
上有最大值为4,设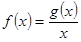 .
.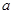 的值;
的值; 在
在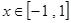 上恒成立,求实数
上恒成立,求实数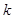 的取值范围.
的取值范围.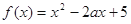 (
(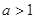 ).
). 的定义域和值域均是
的定义域和值域均是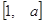 ,求实数
,求实数 的值;
的值;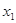 ,
,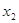
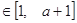 ,总有
,总有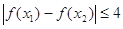 ,求实数
,求实数 的取值范围.
的取值范围. 毫米,滴管内液体忽略不计.
毫米,滴管内液体忽略不计.
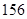 分钟滴完,问每分钟应滴下多少滴?
分钟滴完,问每分钟应滴下多少滴?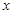 (单位:分钟),瓶内液面与进气管的距离为
(单位:分钟),瓶内液面与进气管的距离为 (单位:厘米),已知当
(单位:厘米),已知当 时,
时,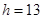 .试将
.试将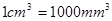 )
) 满足
满足 ,且
,且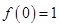 。
。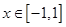 时,方程
时,方程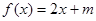 有解,求实数
有解,求实数 的取值范围;
的取值范围;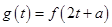 ,
,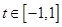 ,求
,求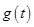 的最大值.
的最大值.