题目内容
已知函数f(x)=为奇函数,f(1)<f(3),
且不等式0≤f(x)≤的解集是{x|-2≤x≤-1或2≤x≤4}.
(1)求a,b,c的值;
(2)是否存在实数m使不等式f(-2+sinθ)<-m2+对一切θ∈R成立?若存在,求出m的取值范围;若不存在,请说明理由.
【答案】
(1)∵f(x)是奇函数,∴f(-x)=-f(x)对定义域内的一切x都成立,
即b=0.
从而f(x)=(x+).
又∵
即
∴f(2)=0,解之,得c=-4.
再由f(1)<f(3),得或从而a>0.
此时f(x)=(x-)
在[2,4]上是增函数.
注意到f(2)=0,则必有f(4)=,∴(4-)=,
即a=2.
综上可知,a=2,b=0,c=-4.
(2)由(1),得f(x)=(x-),该函数在(-∞,0)以及(0,+∞)上均为增函数.
又∵-3≤-2+sinθ≤-1,
∴f(-2+sin θ)的值域为
[-,].
符合题设的实数m应满足-m2>,即m2<0,故符合题设的实数m不存在.
【解析】略

练习册系列答案
相关题目
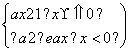 为R上的单调函数,则实数a的取值范围是 ( )
为R上的单调函数,则实数a的取值范围是 ( ) 为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为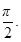
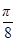 )的值;
)的值; 个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间. 为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
 )的值;
)的值; 个单位后,再将得到的图象上各点的横坐标延长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
个单位后,再将得到的图象上各点的横坐标延长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.