题目内容
已知定义在R上的奇函数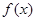 ,满足
,满足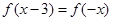 ,且在区间
,且在区间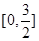 上是增函数,若方程
上是增函数,若方程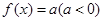 在区间
在区间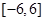 上有四个不同的根
上有四个不同的根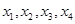 ,则
,则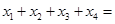
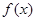 ,满足
,满足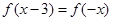 ,且在区间
,且在区间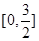 上是增函数,若方程
上是增函数,若方程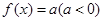 在区间
在区间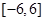 上有四个不同的根
上有四个不同的根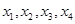 ,则
,则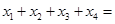
| A.6 | B.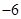 | C.18 | D.0 |
B
试题分析:
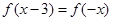 即
即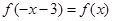 。又奇函数图象关于原点对称,所以如果
。又奇函数图象关于原点对称,所以如果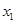 ,
,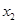 是方程
是方程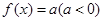 的根,则-
的根,则-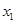 -3,-
-3,-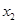 -3也是该方程的根,所以
-3也是该方程的根,所以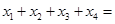 -6,
-6,故选B。
点评:利用函数的奇偶性及图象的对称性,确定得到方程根的关系,从而求得
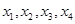 之和。
之和。
练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
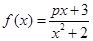 (其中
(其中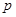 为常数,
为常数,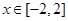 )为偶函数.
)为偶函数.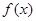 在
在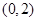 上是单调减函数;
上是单调减函数;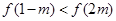 ,求实数
,求实数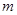 的取值范围.
的取值范围.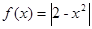 ,若
,若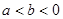 ,且
,且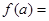
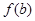 ,则
,则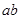 的取值范围是
的取值范围是 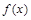 对任意
对任意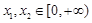
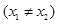 ,有
,有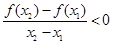 ,则
,则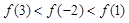
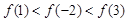
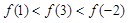
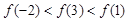
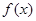 的定义域为
的定义域为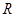 ,
,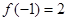 ,对于任意的
,对于任意的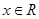 ,
,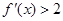 ,则不等式
,则不等式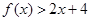 的解集为( )
的解集为( )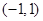
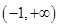
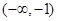
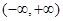
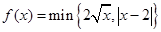 ,其中
,其中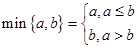 ,若动直线
,若动直线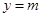 与函数
与函数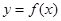 的图像有三个不同的交点,它们的横坐标分别为
的图像有三个不同的交点,它们的横坐标分别为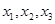 ,则
,则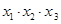 是否存在最大值?若存在,在横线处填写其最大值;若不存在,直接填写“不存在”_______________.
是否存在最大值?若存在,在横线处填写其最大值;若不存在,直接填写“不存在”_______________.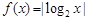 ,正实数
,正实数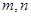 满足
满足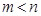 且
且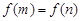 ,若
,若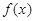 在区间
在区间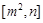 上的最大值为2,则
上的最大值为2,则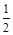 ,2
,2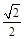 ,
,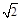
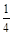 ,2
,2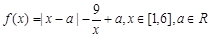 。
。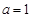 ,试判断并证明
,试判断并证明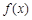 的单调性;
的单调性;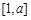 上单调,且存在
上单调,且存在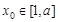 使
使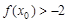 成立,求
成立,求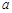 的取值范围;
的取值范围;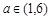 时,求函数
时,求函数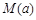 。
。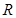 上的函数
上的函数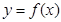 ,对于任意的实数
,对于任意的实数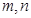 ,恒有
,恒有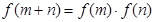 ,且当
,且当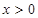 时,
时,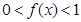 。
。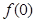 及
及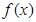 的值域。
的值域。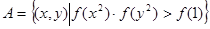 ,
,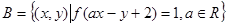 ,
,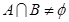 ,求
,求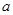 的范围。
的范围。