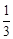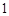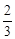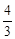题目内容
函数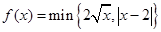 ,其中
,其中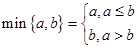 ,若动直线
,若动直线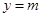 与函数
与函数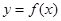 的图像有三个不同的交点,它们的横坐标分别为
的图像有三个不同的交点,它们的横坐标分别为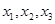 ,则
,则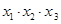 是否存在最大值?若存在,在横线处填写其最大值;若不存在,直接填写“不存在”_______________.
是否存在最大值?若存在,在横线处填写其最大值;若不存在,直接填写“不存在”_______________.
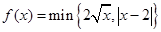 ,其中
,其中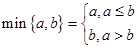 ,若动直线
,若动直线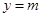 与函数
与函数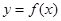 的图像有三个不同的交点,它们的横坐标分别为
的图像有三个不同的交点,它们的横坐标分别为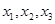 ,则
,则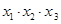 是否存在最大值?若存在,在横线处填写其最大值;若不存在,直接填写“不存在”_______________.
是否存在最大值?若存在,在横线处填写其最大值;若不存在,直接填写“不存在”_______________.1
试题分析:由
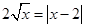 得
得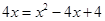 ,即
,即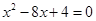 ,解得
,解得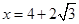 或
或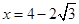 。即
。即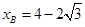 ,
,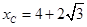 ,所以
,所以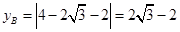 ,所以由图象可知要使直线
,所以由图象可知要使直线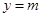 与函数
与函数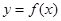 的图像有三个不同的交点,则有
的图像有三个不同的交点,则有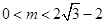 ,即实数
,即实数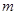 的取值范围是
的取值范围是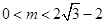 。不妨设
。不妨设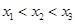 ,则由题意可知
,则由题意可知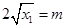 ,所以
,所以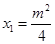 ,由
,由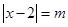 得
得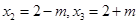 ,所以
,所以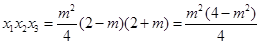 ,因为
,因为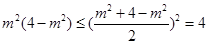 ,所以
,所以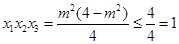 ,即
,即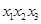 存在最大值,最大值为1.
存在最大值,最大值为1. 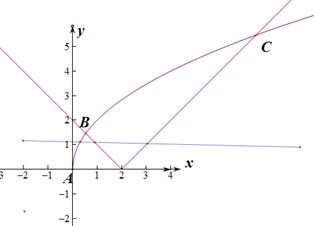
点评:本题主要考查数学结合的数学思想。把
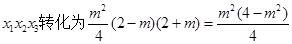 ,然后再利用基本不等式求其最大值,是解题的关键所在。题目难度较大,对学生的要求较高。
,然后再利用基本不等式求其最大值,是解题的关键所在。题目难度较大,对学生的要求较高。
练习册系列答案
相关题目
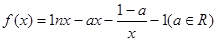 .
.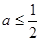 时,讨论
时,讨论 的单调性;
的单调性;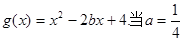 时,若对任意
时,若对任意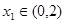 ,存在
,存在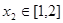 ,使
,使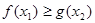 ,求实数
,求实数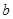 的取值范围.
的取值范围.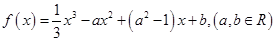 ,其图象在点
,其图象在点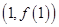 处的切线方程为
处的切线方程为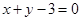
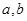 的值;
的值;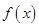 的单调区间,并求出
的单调区间,并求出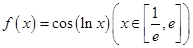 的单调递减区间是 .
的单调递减区间是 .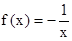 (2)
(2) (3)
(3)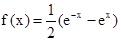
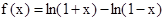 ,其中同时满足:①
,其中同时满足:①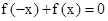 ②对定义域内的任意两个自变量
②对定义域内的任意两个自变量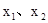 ,都有
,都有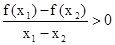 的函数个数为
的函数个数为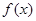 和
和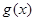 ,其定义域为
,其定义域为 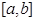 .若对于任意的
.若对于任意的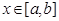 ,总有
,总有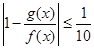 则称
则称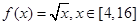 的是 ( )
的是 ( ) 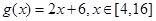
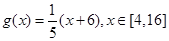
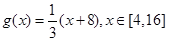
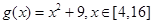
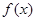 ,满足
,满足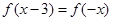 ,且在区间
,且在区间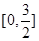 上是增函数,若方程
上是增函数,若方程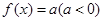 在区间
在区间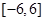 上有四个不同的根
上有四个不同的根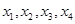 ,则
,则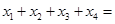
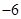
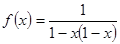 的最大值为( )
的最大值为( )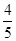
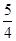
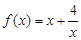 ,且当
,且当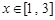 ,
,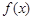 的值域是
的值域是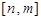 ,则
,则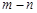 的值是
的值是