题目内容
若函数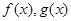 分别是
分别是 上的奇函数、偶函数,且满足
上的奇函数、偶函数,且满足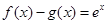 ,则有( )
,则有( )
A. | B. |
C. | D. |
D
解析试题分析:因为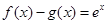 (1),所以
(1),所以 ,又因为函数
,又因为函数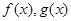 分别是
分别是 上的奇函数、偶函数,所以
上的奇函数、偶函数,所以 (2),(1)+(2)得
(2),(1)+(2)得 ,
,
所以g(0)=-1, ,
, 故选D.
故选D.
考点:1.函数是奇偶性;2.求抽象函数的解析式.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
若函数 ,则下列结论正确的是( )
,则下列结论正确的是( )
A. , , 在 在 上是增函数 上是增函数 |
B. , , 在 在 上是减函数 上是减函数 |
C.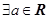 , , 是偶函数 是偶函数 |
D.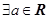 , , 是奇函数 是奇函数 |
在平面直角坐标系中,若P,Q满足条件:(1)P,Q都在函数f(x)的图象上;(2)P,Q两点关于直线y=x对称,则称点对{P,Q}是函数f(x)的一对“可交换点对”.({P,Q}与{Q,P}看作同一“可交换点”.试问函数 的“可交换点对有( )
的“可交换点对有( )
| A.0对 | B.1对 | C.2对 | D.3对 |
设 ,函数
,函数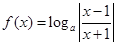 在
在 单调递减,则
单调递减,则 ( )
( )
A.在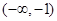 上单调递减,在 上单调递减,在 上单调递增 上单调递增 |
B.在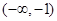 上单调递增,在 上单调递增,在 上单调递减 上单调递减 |
C.在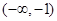 上单调递增,在 上单调递增,在 上单调递增 上单调递增 |
D.在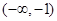 上单调递减,在 上单调递减,在 上单调递减 上单调递减 |
 是R上以2为周期的奇函数,当
是R上以2为周期的奇函数,当 时
时 ,则
,则 在
在 时是( )
时是( )
A.减函数且 | B.减函数且 |
C.增函数且 | D.增函数且 |
已知函数 若关于
若关于 的方程
的方程 有3个不同的实根,则实数
有3个不同的实根,则实数 的取值范围为 ( )
的取值范围为 ( )
A. | B. | C. | D. |
设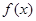 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时,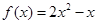 ,则
,则 ( )
( )
A. | B. | C. | D. |
 在
在 上既是奇函数,也是减函数,则
上既是奇函数,也是减函数,则 的图像是( )
的图像是( )
 的图像可能是( )
的图像可能是( ) 


