题目内容
设 ,函数
,函数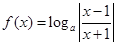 在
在 单调递减,则
单调递减,则 ( )
( )
A.在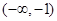 上单调递减,在 上单调递减,在 上单调递增 上单调递增 |
B.在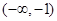 上单调递增,在 上单调递增,在 上单调递减 上单调递减 |
C.在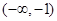 上单调递增,在 上单调递增,在 上单调递增 上单调递增 |
D.在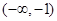 上单调递减,在 上单调递减,在 上单调递减 上单调递减 |
A
解析试题分析:因为当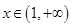 时,
时,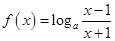 单调递减,由复合函数单调性知,
单调递减,由复合函数单调性知,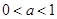 .又函数的定义域为
.又函数的定义域为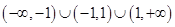 ,关于原点对称且
,关于原点对称且 , 故函数为奇函数,而函数在
, 故函数为奇函数,而函数在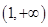 减,由奇函数图象特征得函数在
减,由奇函数图象特征得函数在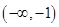 也减,在A,D中选;当
也减,在A,D中选;当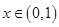 时,
时,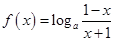 ,因为
,因为 减,
减,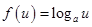 减,故
减,故 增,由于是奇函数,故在
增,由于是奇函数,故在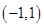 上单调递增,综上可知选A.
上单调递增,综上可知选A.
考点:对数函数、复合函数单调性.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
设 ,则函数
,则函数 的零点位于区间 ( )
的零点位于区间 ( )
| A.(0 ,1) | B.(-1, 0) | C.(1, 2) | D.(2 ,3) |
已知函数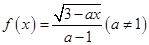 在区间
在区间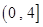 上是增函数,则实数
上是增函数,则实数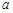 的取值范围是 ( )
的取值范围是 ( )
A.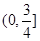 | B.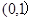 | C.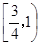 | D.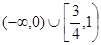 |
已知函数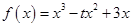 ,若对于任意的
,若对于任意的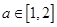 ,
,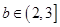 ,函数
,函数 在区间
在区间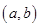 上单调递减,则实数
上单调递减,则实数 的取值范围是( )
的取值范围是( )
A.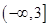 | B.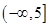 | C.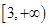 | D.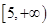 |
若函数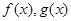 分别是
分别是 上的奇函数、偶函数,且满足
上的奇函数、偶函数,且满足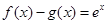 ,则有( )
,则有( )
A. | B. |
C. | D. |
已知函数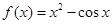 ,对于
,对于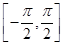 上的任意
上的任意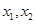 ,有如下条件:①
,有如下条件:①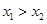 ;②
;②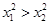 ;③
;③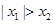 .其中能使
.其中能使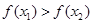 恒成立的条件序号是( )
恒成立的条件序号是( )
| A.①② | B.② | C.②③ | D.③ |
已知函数 的定义域为
的定义域为 ,
, 的定义域为
的定义域为 ,则
,则 ( )
( )
A.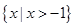 | B.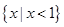 | C. | D. |
对于函数 若
若 则
则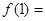 ( )
( )
A.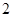 | B. | C. | D. |

