题目内容
 是R上以2为周期的奇函数,当
是R上以2为周期的奇函数,当 时
时 ,则
,则 在
在 时是( )
时是( )
A.减函数且 | B.减函数且 |
C.增函数且 | D.增函数且 |
D
解析试题分析:因为 是R上的奇函数,故
是R上的奇函数,故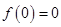 ,由复合函数单调性知,当
,由复合函数单调性知,当 时
时 为增函数,故此时
为增函数,故此时 ;当
;当 时,
时, 为增函数,又因为
为增函数,又因为 是以2为周期的,故在
是以2为周期的,故在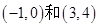 上函数性质和取值完全一样,即
上函数性质和取值完全一样,即 时,
时, 为增函数,选D.
为增函数,选D.
考点:函数奇偶性、函数单调性.

练习册系列答案
相关题目
设函数 有两个极值点
有两个极值点 ,且
,且 ,则 ( )
,则 ( )
A. | B. |
C. | D. |
若函数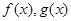 分别是
分别是 上的奇函数、偶函数,且满足
上的奇函数、偶函数,且满足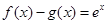 ,则有( )
,则有( )
A. | B. |
C. | D. |
已知函数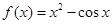 ,对于
,对于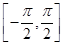 上的任意
上的任意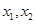 ,有如下条件:①
,有如下条件:①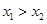 ;②
;②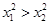 ;③
;③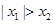 .其中能使
.其中能使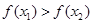 恒成立的条件序号是( )
恒成立的条件序号是( )
| A.①② | B.② | C.②③ | D.③ |
记实数 中的最大数为max{
中的最大数为max{ } , 最小数为min{
} , 最小数为min{ }则max{min{
}则max{min{ }}= ( )
}}= ( )
A. | B.1 | C.3 | D.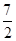 |
已知函数 的定义域为
的定义域为 ,
, 的定义域为
的定义域为 ,则
,则 ( )
( )
A.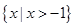 | B.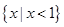 | C. | D. |
已知函数 的定义域为
的定义域为 ,
, 的定义域为
的定义域为 ,则
,则 ( )
( )
A. | B. | C. | D. |


 的图象的交点个数为( )
的图象的交点个数为( )