题目内容
【题目】某家具厂生产一种课桌,每张课桌的成本为50元,出厂单价定为80元,该厂为鼓励销售商多订购,决定一次订购量超过100张时,每超过一张,这批订购的全部课桌出厂单价降低0.02元.根据市场调查,销售商一次订购量不会超过1000张.
(1)设一次订购量为x张,课桌的实际出厂单价为P元,求P关于x的函数关系式P(x);
(2)当一次订购量x为多少时,该家具厂这次销售课桌所获得的利润f(x)最大?其最大利润是多少元?(家具厂售出一张课桌的利润=实际出厂单价﹣成本).
【答案】
(1)解:根据题意得:P(x)= ![]() ;
;
即P(x)= ![]()
(2)解:由(1)得f(x)= ![]()
即f(x)= ![]()
(ⅰ)当0<x≤100,
则x=100时,f(x)max=f(100)=3000)
(ⅱ)当100<x≤1000,
则x=800时,f(x)max=f(800)=32×800﹣0.02×8002=12800
∵12800>3000,
∴x=800时,f(x)有最大值,其最大值为12800元.
答:当一次订购量为800张时,该家具厂在这次订购中所获得的利润最大,其最大利润是12800元
【解析】(1)当0<x≤100时,P=80;当100<x≤1000时,P=80﹣0.02(x﹣100),由此可得分段函数;(2)利用工厂售出一个零件的利润=实际出厂单价﹣成本,即可求出当销售商一次订购了800个零件时,该厂获得的利润.

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案【题目】某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
学习积极性高 | 18 | 7 | 25 |
学习积极性一般 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
参考公式及数据: 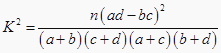
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(2)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关系?并说明理由?