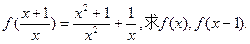题目内容
已知函数f(x)＝－xm，且f(4)＝－.
(1)求m的值；
(2)判断f(x)在(0，＋∞)上的单调性，并给予证明
(1)∵f(4)＝－，
∴－4m＝－，∴m＝1.
(2)f(x)＝－x在(0，＋∞)上单调递减，证明如下：
任取0＜x1＜x2，
则f(x1)－f(x2)
＝(－x1)－(－x2)
＝(x2－x1)(＋1)．
∵0＜x1＜x2，∴x2－x1＞0，＋1＞0.
∴f(x1)－f(x2)＞0，
∴f(x1)＞f(x2)，
即f(x)＝－x在(0，＋∞)上单调递减．
解析
练习册系列答案
相关题目
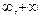)上的单调性，并用定义证明。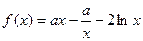
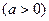，若函数
在其定义域内为单调函数，求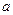
的取值范围.
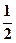,1]时，不等式f (ax+1)≤f (x－2)恒成立，则求实数a的取值范围？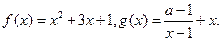
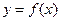和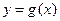
的公共点个数；
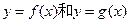的公共点个数恰为两个。
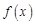和
的图象关于原
点对称，且
．
；
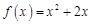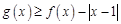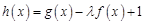在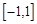
上是增函数，求实数
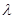的取值范围．
)已知