题目内容
对于定义域为D的函数y=f(x),如果存在区间[m,n]⊆D,同时满足下列条件:①f(x)在[m,n]内是单调的;②当定义域是[m,n]时,f(x)的值域也是[m,n]时,则称[m,n]是该函数的“和谐区间”.(1)判断函数
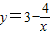 是否存在“和谐区间”,并说明理由;
是否存在“和谐区间”,并说明理由;(2)如果[m,n]是函数
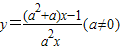 的一个“和谐区间”,求n-m的最大值;
的一个“和谐区间”,求n-m的最大值;(3)有些函数有无数个“和谐区间”,如y=x,请你再举一类(无需证明)
【答案】分析:(1)该问题是一个判断性问题,从正面证明有一定的难度,故可采用反证法来进行证明,即先假设区间[m,n]为函数的“和谐区间”,然后根据函数的性质得到矛盾,进而得到假设不成立,原命题成立.
(2)设[m,n]是已知函数定义域的子集,我们可以用a表示出n-m的取值,转化为二次函数的最值问题后,根据二次函数的性质,可以得到答案.
(3)根据“和谐区间”的定义,我们还可以写出以下函数:y=a-x(a为常数),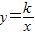 (k>o为常数)满足有无数个“和谐区间”.
(k>o为常数)满足有无数个“和谐区间”.
解答:解:(1)设[m,n]是函数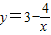 的“和谐区间”,则
的“和谐区间”,则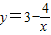 在[m,n]上单调.
在[m,n]上单调.
所以[m,n]⊆(-∞,0)或[m,n]⊆(0,+∞)
因此,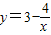 在[m,n]上为增函数.
在[m,n]上为增函数.
则f(m)=m,f(n)=n.即方程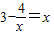 有两个解m,n
有两个解m,n
又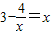 可化为x2-3x+4=0,而x2-3x+4=0无实数解.
可化为x2-3x+4=0,而x2-3x+4=0无实数解.
所以,函数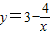 不存在“和谐区间”
不存在“和谐区间”
(2)因为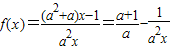 在[m,n]上是单调的,
在[m,n]上是单调的,
所以[m,n]⊆(-∞,0)或[m,n]⊆(0,+∞)
则f(m)=m,f(n)=n
所以m,n是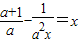 的两个同号的实数根
的两个同号的实数根
即方程a2x-(a2+a)x+1=0有两个同号的实数根,注意到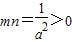
只要△=(a2+a)2-4a2>0,解得a>1或a<-3
所以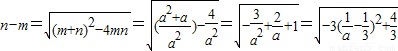
其中a>1或a<-3,所以,当a=3时,n-m取最大值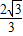
(3)答案不唯一,如可写出以下函数:y=a-x(a为常数),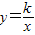 (k>0为常数)
(k>0为常数)
点评:本题主要以新定义为载体,综合考查了函数的单调性、函数的最值方程的根的情况、二次函数的最值的求解,考查了利用已学知识解决新问题的能力,考查了推理运算的能力,本题综合性较强.
(2)设[m,n]是已知函数定义域的子集,我们可以用a表示出n-m的取值,转化为二次函数的最值问题后,根据二次函数的性质,可以得到答案.
(3)根据“和谐区间”的定义,我们还可以写出以下函数:y=a-x(a为常数),
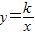 (k>o为常数)满足有无数个“和谐区间”.
(k>o为常数)满足有无数个“和谐区间”.解答:解:(1)设[m,n]是函数
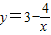 的“和谐区间”,则
的“和谐区间”,则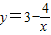 在[m,n]上单调.
在[m,n]上单调.所以[m,n]⊆(-∞,0)或[m,n]⊆(0,+∞)
因此,
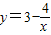 在[m,n]上为增函数.
在[m,n]上为增函数.则f(m)=m,f(n)=n.即方程
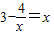 有两个解m,n
有两个解m,n又
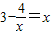 可化为x2-3x+4=0,而x2-3x+4=0无实数解.
可化为x2-3x+4=0,而x2-3x+4=0无实数解.所以,函数
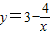 不存在“和谐区间”
不存在“和谐区间”(2)因为
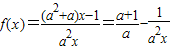 在[m,n]上是单调的,
在[m,n]上是单调的,所以[m,n]⊆(-∞,0)或[m,n]⊆(0,+∞)
则f(m)=m,f(n)=n
所以m,n是
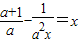 的两个同号的实数根
的两个同号的实数根即方程a2x-(a2+a)x+1=0有两个同号的实数根,注意到
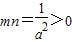
只要△=(a2+a)2-4a2>0,解得a>1或a<-3
所以
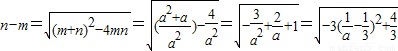
其中a>1或a<-3,所以,当a=3时,n-m取最大值
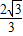
(3)答案不唯一,如可写出以下函数:y=a-x(a为常数),
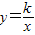 (k>0为常数)
(k>0为常数)点评:本题主要以新定义为载体,综合考查了函数的单调性、函数的最值方程的根的情况、二次函数的最值的求解,考查了利用已学知识解决新问题的能力,考查了推理运算的能力,本题综合性较强.

练习册系列答案
相关题目