Question

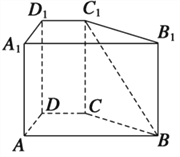
【题目】如图，在四棱锥中P﹣ABCD，AB=BC=CD=DA，∠BAD=60°，AQ=QD，△PAD是正三角形．

（1）求证：AD⊥PB；

（2）已知点M是线段PC上，MC=λPM，且PA∥平面MQB，求实数λ的值．

Answer 1

【答案】（1）见解析；（2）2.

【解析】

（1）连结BD，则△ABD为正三角形，从而AD⊥BQ，AD⊥PQ，进而AD⊥平面PQB，由此能证明AD⊥PB；

（2）连结AC，交BQ于N，连结MN，由AQ∥BC，得，根据线面平行的性质定理得MN∥PA，由此能求出实数λ的值．

证明：（1）如图，连结BD，由题意知四边形ABCD为菱形，∠BAD=60°，

∴△ABD为正三角形，

又∵AQ=QD，∴Q为AD的中点，∴AD⊥BQ，

∵△PAD是正三角形，Q为AD中点，

∴AD⊥PQ，又BQ∩PQ=Q，∴AD⊥平面PQB，

又∵PB平面PQB，∴AD⊥PB．

解：（2）连结AC，交BQ于N，连结MN，

∵AQ∥BC，∴，

∵PN∥平面MQB，PA平面PAC，

平面MQB∩平面PAC=MN，

∴根据线面平行的性质定理得MN∥PA，

∴，

综上，得，∴MC=2PM，∵MC=λPM，∴实数λ的值为2．