Question

【题目】选修4﹣1：几何证明选讲
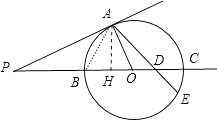
如图，已知PA是⊙O的切线，A是切点，直线PO交⊙O于B、C两点，D是OC的中点，连接AD并延长交⊙O于点E，若PA=2 ，∠APB=30°．

（1）求∠AEC的大小；
（2）求AE的长．

Answer 1

【答案】
（1）解：连接AB，因为：∠APO=30°，且PA是⊙O的切线，

所以：∠AOB=60°；

∵OA=OB

∴∠AB0=60°；

∵∠ABC=∠AEC

∴∠AEC=60°．

（2）解：由条件知AO=2，过A作AH⊥BC于H，则AH= ，

在RT△AHD中，HD=2，∴AD= = ．

∵BDDC=ADDE，

∴DE= ．

∴AE=DE+AD= ．

【解析】（1）先连接AB，根据切线的性质以及已知条件得到：∠AOB=60°；再结合OA=OB以及∠ABC=∠AEC即可得到结论；（2）分两段，先根据直角三角形中的有关性质求出AD，再结合相交弦定理求出DE，二者相加即可．