Question

如图（1），在三角形ABC中，AB⊥AC，若AD⊥BC，则AB²=BD．BC；若类比该命题，如图（2），三棱锥A-BCD中，AD⊥面ABC，若A点在三角形BCD所在平面内的射影为M，则有什么结论？命题是否是真命题．

Answer 1

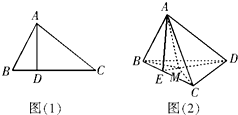
命题是：三棱锥A-BCD中，AD⊥面ABC，若A点在三角形BCD所在平面内的射影为M，
则有S_△ABC²=S_△BCM•S_△BCD是一个真命题．
证明如下：
在图（2）中，连接DM，并延长交BC于E，连接AE，则有DE⊥BC．
因为AD⊥面ABC，所以AD⊥AE．
又AM⊥DE，所以AE²=EM•ED．
于是S△ABC2=(

1

2

BC•AE)2(

1

2

BC•EM)•(

1

2

BC•ED)=S_△BCM•S_△BCD．
故有S_△ABC²=S_△BCM•S_△BCD