题目内容
若直线ax+by=1与圆x2+y2=1相切,则实数ab的取值范围是________.

分析:先用原点到直线的距离等于半径,得到a、b的关系,再用基本不等式确定ab的范围.
解答:直线ax+by=1与圆x2+y2=1相切,则、
即:a2+b2=1,∵a2+b2≥2|ab|
∴2|ab|≤1?
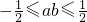
故答案为:

点评:本题考查直线与圆的位置关系,基本不等式,此式a2+b2≥2|ab|是易出错点,本题是考查学生能力的小题.

练习册系列答案
相关题目
若直线ax+by+1=0(a、b>0)过圆x2+y2+8x+2y+1=0的圆心,则
+
的最小值为( )
| 1 |
| a |
| 4 |
| b |
| A、8 | B、12 | C、16 | D、20 |