题目内容
20.已知a,b,c分别是△ABC的三个内角A,B,C的对边,asinA=bsinB+(c-b)sinC.(Ⅰ)求角A的大小;
(Ⅱ)求函数f(x)=2$\sqrt{3}$cos2$\frac{B}{2}$-sin(C-$\frac{π}{3}$)的值域.
分析 (Ⅰ)原式由正弦定理化简可得a2=b2-bc,从而有余弦定理并结合A的范围即可求得A的值.
(Ⅱ)由三角函数中的恒等变换应用化简解析式可得f(x)=sin(B+$\frac{π}{3}$)+$\sqrt{3}$,结合角B的范围及正弦函数的单调性即可得解.
解答 (本题满分12分)
解:(Ⅰ)asinA=bsinB+(c-b)sinC.
⇒2RasinA=2RbsinB+2R(c-b)sinC
⇒a2=b2-bc
⇒cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}=\frac{1}{2}$
⇒A=$\frac{π}{3}$…5分
(Ⅱ)f(x)=2$\sqrt{3}$cos2$\frac{B}{2}$-sin(C$\frac{π}{3}$)=$\sqrt{3}$(cosB+1)-sin($\frac{π}{3}-B$)
=$\sqrt{3}$cosB+$\sqrt{3}$-$\frac{\sqrt{3}}{2}$cosB+$\frac{1}{2}$sinB
=$\frac{1}{2}$sinB+$\frac{\sqrt{3}}{2}$cosB+$\sqrt{3}$
=sin(B+$\frac{π}{3}$)+$\sqrt{3}$…8分
由于0$<B<\frac{2π}{3}$⇒$\frac{π}{3}<B+\frac{π}{3}<π$⇒$\sqrt{3}<f(x)≤1+\sqrt{3}$,
所以函数f(x)=2$\sqrt{3}$cos2$\frac{B}{2}$-sin(C-$\frac{π}{3}$)的值域为($\sqrt{3}$,$\sqrt{3}+1$]…12分
点评 本题主要考查了正弦定理,余弦定理,三角函数中的恒等变换应用,解题时注意角的范围的讨论,属于基本知识的考查.

| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{2}}{2}$ | D. | -$\frac{1}{2}$ |
| A. | (1,4) | B. | (-1,1) | C. | (1,+∞) | D. | (-1,+∞) |
| A. | $A_6^2×A_5^4$种 | B. | $A_6^2×{5^4}$种 | C. | $C_6^2×A_5^4$种 | D. | $C_6^2×{5^4}$种 |
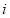 是虚数单位,若复数
是虚数单位,若复数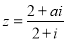 在复平面内对应的点在第四象限,则实数
在复平面内对应的点在第四象限,则实数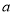 的值可以是( )
的值可以是( )