题目内容
5. 如图,在四棱锥A-DCBE中,AC⊥BC,底面DCBE为平行四边形,DC⊥平面ABC.
如图,在四棱锥A-DCBE中,AC⊥BC,底面DCBE为平行四边形,DC⊥平面ABC.(Ⅰ)求证:DE⊥平面ACD;
(Ⅱ)设平面ADE∩平面ABC=直线l,求证:BC∥l;
(Ⅲ)若∠ABC=30°,AB=2,EB=$\sqrt{3}$,求三棱锥B-ACE的体积.
分析 (Ⅰ)利用线面垂直的判定定理证明BC⊥平面ACD,利用底面DCBE为平行四边形,所以BC∥ED,可得DE⊥平面ACD;
(Ⅱ)证明BC∥平面ADE,利用平面ADE∩平面ABC=直线l,可得BC∥l;
(Ⅲ)证明BE⊥平面ABC,利用VB-ACE=VE-ABC,求三棱锥B-ACE的体积.
解答 (Ⅰ)证明:因为DC⊥平面ABC,BC?平面ABC,所以BC⊥DC.…(1分)
又因为AC⊥BC,AC?平面ACD,CD?平面ACD,AC∩CD=C,
所以,BC⊥平面ACD.…(3分)
因为底面DCBE为平行四边形,所以BC∥ED.
所以DE⊥平面ACD.…(5分)
(Ⅱ)证明:因为底面DCBE为平行四边形,所以BC∥ED.…(6分)
因为BC?平面ADE,ED?平面ADE,所以BC∥平面ADE.…(8分)
因为平面ADE∩平面ABC=l,BC?平面ABC,所以BC∥l.…(10分)
(Ⅲ)解:因为底面DCBE为平行四边形,DC⊥平面ABC,
所以BE⊥平面ABC.
所以VB-ACE=VE-ABC=$\frac{1}{3}×\frac{1}{2}×1×\sqrt{3}×\sqrt{3}=\frac{1}{2}$.…(12分)
点评 本题考查线面垂直的判定,考查线面平行,三棱锥体积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.直线y=kx与椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)交于A、B两点,F为椭圆C的左焦点,且$\overrightarrow{AF}$•$\overrightarrow{BF}$=0,若∠ABF∈(0,$\frac{π}{12}$],则椭圆C的离心率的取值范围是( )
| A. | (0,$\frac{\sqrt{2}}{2}$] | B. | (0,$\frac{\sqrt{6}}{3}$] | C. | [$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{6}}{3}$] | D. | [$\frac{\sqrt{6}}{3}$,1) |
17.若一球的表面积为8π,则它的体积为( )
| A. | $\frac{4\sqrt{2}π}{3}$ | B. | $\frac{8\sqrt{2}π}{3}$ | C. | $\frac{32π}{3}$ | D. | $\frac{16π}{3}$ |

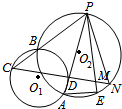 如图,已知⊙O1与⊙O2相交于A、B两点,P是⊙O1上一点,PB的延长线交⊙O2于点C,PA交⊙O2于点D,CD的延长线交⊙O1于点N.
如图,已知⊙O1与⊙O2相交于A、B两点,P是⊙O1上一点,PB的延长线交⊙O2于点C,PA交⊙O2于点D,CD的延长线交⊙O1于点N.