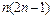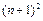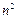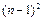题目内容
(本小题满分13分)
已知数列{an}的前n项和为Sn,Sn=2-(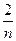 +1)an(n≥1).
+1)an(n≥1).
(1)求证:数列{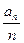 }是等比数列;
}是等比数列;
(2)设数列{2nan}的前n项和为Tn,An=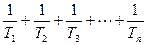 .试比较An与
.试比较An与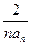 的大小。
的大小。
已知数列{an}的前n项和为Sn,Sn=2-(
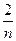 +1)an(n≥1).
+1)an(n≥1).(1)求证:数列{
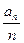 }是等比数列;
}是等比数列;(2)设数列{2nan}的前n项和为Tn,An=
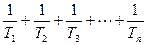 .试比较An与
.试比较An与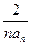 的大小。
的大小。解:(1)由a1=S1=2-3a1得a1=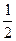 ,
,  1分
1分
由Sn=2-(
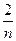 +1)an得Sn-1=2-(
+1)an得Sn-1=2-(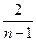 +1)an-1,
+1)an-1,
于是an=Sn- Sn-1=(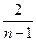 +1)an-1-(
+1)an-1-(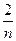 +1)an,
+1)an,
整理得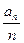 =
=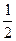 ×
×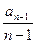 (n≥2), 4分
(n≥2), 4分
所以数列{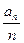 }是首项及公比均为
}是首项及公比均为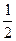 的等比数列. 5分
的等比数列. 5分
(2)由(Ⅰ)得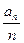 =
=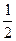 ×
×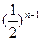 =
=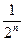 . 6分
. 6分
于是2nan=n,Tn=1+2+3+…+n=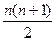 , 7分
, 7分
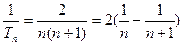 ,
,
An=2[(1-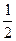 )+(
)+(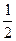 -
-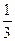 )+…+
)+…+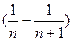 =2(1-
=2(1-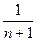 )=
)=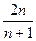 .
.
9分
又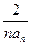 =
=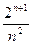 ,问题转化为比较
,问题转化为比较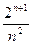 与
与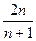 的大小,即
的大小,即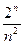 与
与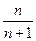 的大小.
的大小.
设f(n)=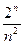 ,g(n)=
,g(n)=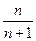 .
.
∵f(n+1)-f(n)=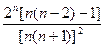 ,当n≥3时, f(n+1)-f(n)>0,
,当n≥3时, f(n+1)-f(n)>0,
∴当n≥3时f(n)单调递增, 11分
∴当n≥4时,f(n) ≥f(4)=1,而g(n)<1, ∴当n≥4时f(n) >g(n),
经检验n=1,2,3时,仍有f(n) ≥g(n),
因此,对任意正整数n,都有f(n) >g(n),
即An <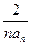 . 13分
. 13分
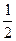 ,
,  1分
1分由Sn=2-(

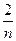 +1)an得Sn-1=2-(
+1)an得Sn-1=2-(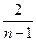 +1)an-1,
+1)an-1,于是an=Sn- Sn-1=(
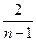 +1)an-1-(
+1)an-1-(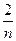 +1)an,
+1)an,整理得
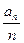 =
=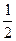 ×
×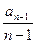 (n≥2), 4分
(n≥2), 4分所以数列{
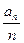 }是首项及公比均为
}是首项及公比均为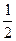 的等比数列. 5分
的等比数列. 5分(2)由(Ⅰ)得
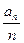 =
=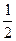 ×
×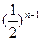 =
=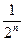 . 6分
. 6分于是2nan=n,Tn=1+2+3+…+n=
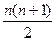 , 7分
, 7分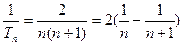 ,
,An=2[(1-
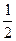 )+(
)+(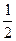 -
-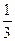 )+…+
)+…+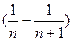 =2(1-
=2(1-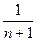 )=
)=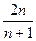 .
.9分
又
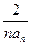 =
=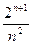 ,问题转化为比较
,问题转化为比较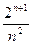 与
与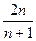 的大小,即
的大小,即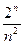 与
与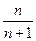 的大小.
的大小.设f(n)=
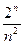 ,g(n)=
,g(n)=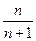 .
.∵f(n+1)-f(n)=
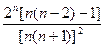 ,当n≥3时, f(n+1)-f(n)>0,
,当n≥3时, f(n+1)-f(n)>0,∴当n≥3时f(n)单调递增, 11分
∴当n≥4时,f(n) ≥f(4)=1,而g(n)<1, ∴当n≥4时f(n) >g(n),
经检验n=1,2,3时,仍有f(n) ≥g(n),
因此,对任意正整数n,都有f(n) >g(n),
即An <
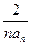 . 13分
. 13分略

练习册系列答案
相关题目
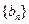 满足
满足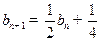 ,且
,且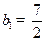 ,
, 为
为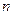 项和.
项和.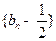 是等比数列,并求
是等比数列,并求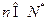 ,不等式
,不等式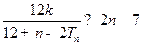 恒成立,求实数
恒成立,求实数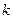 的取值范围.
的取值范围.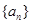 是公比为q的等比数列,
是公比为q的等比数列,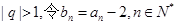 ,若数列
,若数列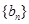 有连续四项在集合
有连续四项在集合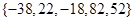 中,则
中,则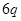 = ( )
= ( )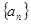 的公比
的公比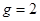 ,道项
,道项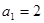 ,则
,则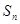 等于( )
等于( )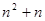
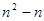
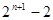
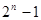
 ,若
,若 +
+ =20,
=20, +
+ =80,则
=80,则 +
+ 等于
等于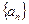 中,
中,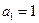 ,公比
,公比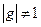 ,若
,若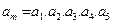 ,则m=
,则m=
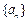 满足
满足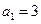 ,且
,且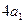 ,
,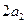 ,
,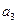 成等差数列,则
成等差数列,则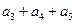 =" " ( )
=" " ( )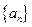 的前
的前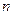 项和为
项和为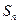 ,若
,若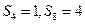 ,则
,则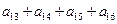 等于( )
等于( )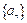 满足
满足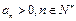 ,且
,且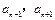 是方程
是方程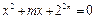 的两个实根,则当
的两个实根,则当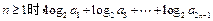 等于 ( )
等于 ( )