题目内容
(本小题满分12分)
已知数列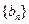 满足
满足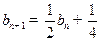 ,且
,且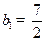 ,
, 为
为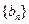 的前
的前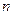 项和.
项和.
(Ⅰ)求证:数列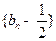 是等比数列,并求
是等比数列,并求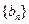 的通项公式;
的通项公式;
(Ⅱ)如果对任意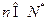 ,不等式
,不等式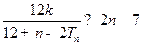 恒成立,求实数
恒成立,求实数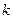 的取值范围.
的取值范围.
已知数列
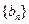 满足
满足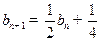 ,且
,且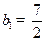 ,
, 为
为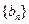 的前
的前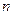 项和.
项和.(Ⅰ)求证:数列
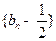 是等比数列,并求
是等比数列,并求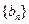 的通项公式;
的通项公式;(Ⅱ)如果对任意
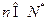 ,不等式
,不等式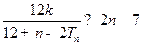 恒成立,求实数
恒成立,求实数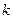 的取值范围.
的取值范围.解:(Ⅰ)对任意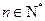 ,都有
,都有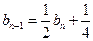 ,所以
,所以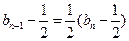
则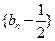 成等比数列,首项为
成等比数列,首项为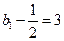 ,公比为
,公比为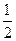 …………2分
…………2分
所以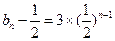 ,
,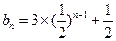 …………4分
…………4分
(Ⅱ)因为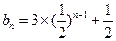
所以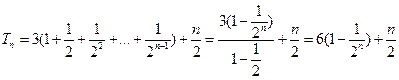 …………6分
…………6分
因为不等式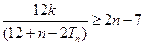 ,化简得
,化简得 对任意
对任意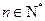 恒成立…………7分
恒成立…………7分
设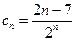 ,则
,则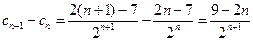 …………8分
…………8分
当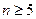 ,
,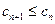 ,
, 为单调递减数列,当
为单调递减数列,当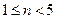 ,
,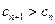 ,
, 为单调递增数列
为单调递增数列
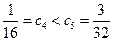 ,所以,
,所以,  时,
时, 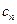 取得最大值
取得最大值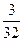 …………11分
…………11分
所以, 要使 对任意
对任意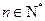 恒成立,
恒成立,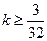 …………12分
…………12分
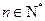 ,都有
,都有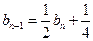 ,所以
,所以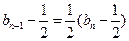
则
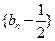 成等比数列,首项为
成等比数列,首项为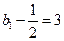 ,公比为
,公比为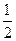 …………2分
…………2分所以
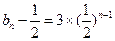 ,
,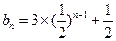 …………4分
…………4分(Ⅱ)因为
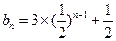
所以
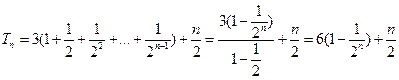 …………6分
…………6分因为不等式
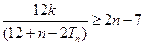 ,化简得
,化简得 对任意
对任意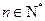 恒成立…………7分
恒成立…………7分设
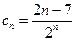 ,则
,则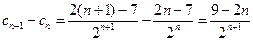 …………8分
…………8分当
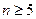 ,
,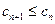 ,
, 为单调递减数列,当
为单调递减数列,当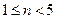 ,
,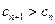 ,
, 为单调递增数列
为单调递增数列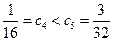 ,所以,
,所以,  时,
时, 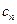 取得最大值
取得最大值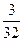 …………11分
…………11分所以, 要使
 对任意
对任意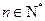 恒成立,
恒成立,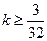 …………12分
…………12分略

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
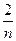 +1)an(n≥1).
+1)an(n≥1).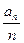 }是等比数列;
}是等比数列;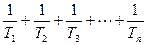 .试比较An与
.试比较An与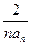 的大小。
的大小。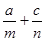 等于
等于 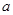 元,若每到第二年的这一天取出,再连本带利存入银行(假设银行年利率为
元,若每到第二年的这一天取出,再连本带利存入银行(假设银行年利率为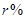 ),则到2015年1月5日他共可取出款
),则到2015年1月5日他共可取出款 (元)
(元)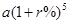 (元)
(元) (元)
(元)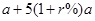 (元)
(元)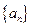 的前
的前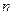 项和为
项和为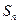 ,点
,点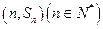 在函数
在函数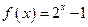 的图象上,则数列
的图象上,则数列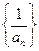 的前
的前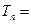 _______________
_______________ 中,
中, ,且
,且 ,则
,则 等于( )
等于( ) 中
中 ,若
,若 ,
, 则数列
则数列 = ( )
= ( )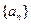 中,已知
中,已知 ,那么
,那么 =( )
=( )