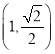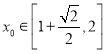题目内容
【题目】已知圆![]() ,过直线
,过直线![]() 上第一象限内的一动点
上第一象限内的一动点![]() 作圆
作圆![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,过
,过![]() 两点的直线与坐标轴分别交于
两点的直线与坐标轴分别交于![]() 两点,则
两点,则![]() 面积的最小值为( )
面积的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
由切线的性质,结合四点共圆判断可得O,A,M,B四点共圆,求得圆方程,由两圆方程相减可得相交弦AB方程,由题意可得![]() 面积,结合基本不等式求得最值.
面积,结合基本不等式求得最值.
因为AB为切点,所以OA⊥AM,OB⊥BM,
所以O,A,M,B四点共圆,设M(![]() ,
,![]() ),
),
则其圆心O'(![]() ,
,![]() ),方程为(x
),方程为(x![]() )2+(y
)2+(y![]() )2
)2![]() ,
,
整理得x2+y2﹣xx0﹣yy0=0,与圆O:x2+y2=1的方程作差得x![]() + y
+ y![]() =1,
=1,
又AB是圆O与圆O'的公共弦,
即直线AB的方程为x![]() + y
+ y![]() =1,
=1,
又过![]() 两点的直线与坐标轴分别交于
两点的直线与坐标轴分别交于![]() 两点,
两点,
得P(![]() ,0)Q(0,
,0)Q(0,![]() ),又
),又![]() +
+![]() =2
=2![]() ,∴
,∴![]() ,当且仅当
,当且仅当![]() =
=![]() =1等号成立,
=1等号成立,
则![]() 面积为
面积为![]() ,∴
,∴![]() 面积的最小值为
面积的最小值为![]()
故选:B.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目