题目内容
在正三棱柱ABC—A1B1C1中，各棱长都是a,D、E分别是AC1、BB1的中点.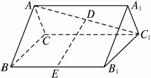
(1)求证：DE是异面直线AC1、BB1的公垂线段，并求其长度；
(2)求二面角E-AC1-C的大小；
(3)求点C1到平面AEC的距离.
(1)证明：过D在面AC1内作FG∥A1C1分别交AA1、CC1于F、G，则面EFG∥面ABC∥面A1B1C1，D为FG中点，ED⊥FG，面EFG⊥面AC1.?
又面EFG⊥BB1，∴ED⊥BB1.?
故DE是异面直线AC1、BB1的公垂线段，DE=
a.?
(2)解析：容易证得CD⊥AC1，又由上小题可知DE⊥AC1,∴∠CDE为二面角E-AC1-C的平面角.
可得∠CDE=90°，故二面角E-AC1-C为90°.?
(3)解析：用体积法可得点C1到平面AEC的距离为
a.
练习册系列答案
相关题目
如图，在正三棱柱ABC-A1B1C1中，AA1=AB，D是AC的中点．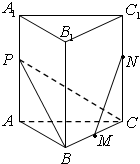
如图，在正三棱柱ABC-A1B1C1中，所有棱的长度都是1，M是BC边的中点，P是AA1边上的点，且
如图，在正三棱柱ABC-A'B'C'中，AB=2，若二面角C'-AB-C的大小为60°，则点C到平面ABC'的距离为