题目内容
13．己知数列{an}的通项为an=$\frac{n}{{2}^{n-1}}$，则它的前n项和Sn=4-$\frac{4+2n}{{2}^{n}}$．分析 利用“错位相减法”、等比数列的前n项和公式即可得出．
解答 解：∵数列{an}的通项为an=$\frac{n}{{2}^{n-1}}$，
∴它的前项和Sn=1+$\frac{2}{2}+\frac{3}{{2}^{2}}$+…+$\frac{n}{{2}^{n-1}}$，
$\frac{1}{2}{S}_{n}$=$\frac{1}{2}+\frac{2}{{2}^{2}}$+$\frac{3}{{2}^{3}}$+…+$\frac{n-1}{{2}^{n-1}}$+$\frac{n}{{2}^{n}}$，
∴$\frac{1}{2}{S}_{n}$=1+$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n-1}}$-$\frac{n}{{2}^{n}}$=$\frac{1-\frac{1}{{2}^{n}}}{1-\frac{1}{2}}$-$\frac{n}{{2}^{n}}$=2-$\frac{2+n}{{2}^{n}}$，
∴Sn=4-$\frac{4+2n}{{2}^{n}}$．
故答案为：4-$\frac{4+2n}{{2}^{n}}$．
点评 本题考查了“错位相减法”、等比数列的前n项和公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
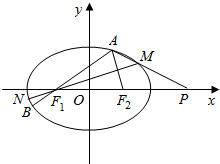已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{2}}{2}$．A为椭圆C上一动点（A异于左、右顶点），F1、F2分别为椭圆C的左、右焦点，且△AF1F2面积的最大值为1；