题目内容
3.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{2}$=1的一个焦点与抛物线y2=8x的焦点重合,则该双曲线的实轴长等于2$\sqrt{2}$.分析 求出双曲线的焦点坐标,抛物线的焦点坐标,然后求解实轴的长.
解答 解:抛物线y2=8x的焦点(2,0)是双曲线$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{2}$=1的一个焦点,
所以c=2,可得a2+2=22,解得a=$\sqrt{2}$.
双曲线的实轴长为:2$\sqrt{2}$.
故答案为:2$\sqrt{2}$.
点评 本题考查抛物线与双曲线的简单性质的应用,基本知识的考查.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
18.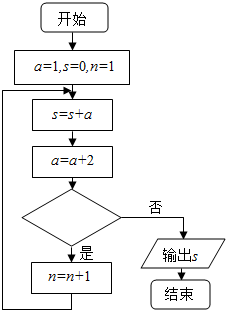 阅读如图所示的程序框图,运行相应的程序,若输出的结果s=9,则图中菱形内应该填写的内容是( )
阅读如图所示的程序框图,运行相应的程序,若输出的结果s=9,则图中菱形内应该填写的内容是( )
 阅读如图所示的程序框图,运行相应的程序,若输出的结果s=9,则图中菱形内应该填写的内容是( )
阅读如图所示的程序框图,运行相应的程序,若输出的结果s=9,则图中菱形内应该填写的内容是( )| A. | n<2 | B. | n<3 | C. | n<4 | D. | a<3 |