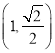题目内容
【题目】已知椭圆![]() 过点
过点![]() ,且离心率
,且离心率![]() .
.
(Ⅰ)求椭圆![]() 的方程.
的方程.
(Ⅱ)若椭圆![]() 上存在点
上存在点![]() 、
、![]() 关于直线
关于直线![]() 对称,求
对称,求![]() 的所有取值构成的集合
的所有取值构成的集合![]() ,并证明对于
,并证明对于![]() ,
, ![]() 的中点恒在一条定直线上.
的中点恒在一条定直线上.
【答案】(![]() )
)![]() .(
.(![]() )见解析
)见解析
【解析】试题分析:(Ⅰ)因为 椭圆![]() 过点
过点![]() ,所以
,所以![]() .因为
.因为![]() , 所以
, 所以![]() .所以椭圆
.所以椭圆![]() 的方程为
的方程为![]() ;(Ⅱ)依题意得
;(Ⅱ)依题意得![]() .因为 椭圆
.因为 椭圆![]() 上存在点
上存在点![]() 关于直线
关于直线![]() 对称,所以 直线
对称,所以 直线![]() 与直线
与直线![]() 垂直,且线段
垂直,且线段![]() 的中点在直线
的中点在直线![]() 上.
上.
设直线![]() 的方程为
的方程为![]() .由
.由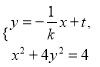 得
得![]() ,由
,由![]() 得
得![]() ①,
①, ![]() 的中点坐标为
的中点坐标为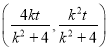 所以
所以![]() ,所以
,所以![]() 代入①得
代入①得![]() 或
或![]() ,所以
,所以![]() 或
或
![]() 因为
因为![]() ,所以 对于
,所以 对于![]() ,线段
,线段![]() 中点的纵坐标恒为
中点的纵坐标恒为![]() ,即线段
,即线段![]() 的中点总在直线
的中点总在直线![]() 上.
上.
试题解析:(Ⅰ)因为 椭圆![]() 过点
过点![]() ,
,
所以![]() . 1分
. 1分
因为![]() ,
,
所以![]() .
.
所以 椭圆![]() 的方程为
的方程为![]() 3分
3分
(Ⅱ)方法一:
依题意得![]() .
.
因为 椭圆![]() 上存在点
上存在点![]() 关于直线
关于直线![]() 对称,
对称,
所以 直线![]() 与直线
与直线![]() 垂直,且线段
垂直,且线段![]() 的中点在直线
的中点在直线![]() 上.
上.
设直线![]() 的方程为
的方程为![]() .
.
由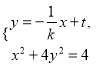 得
得![]() . 5分
. 5分
由![]() ,
,
得![]() .(*)
.(*)
因为![]() , 7分
, 7分
所以![]() 的中点坐标为
的中点坐标为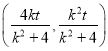 .
.
又线段![]() 的中点在直线
的中点在直线![]() 上,
上,
所以![]() .
.
所以![]() . 9分
. 9分
代入(*),得![]() 或
或![]() .
.
所以![]() 或
或![]() . 11分
. 11分
因为![]() ,
,
所以 对于![]() ,线段
,线段![]() 中点的纵坐标恒为
中点的纵坐标恒为![]() ,即线段
,即线段![]() 的中点总在直线
的中点总在直线![]() 上.
上.
13分
方法二:
因为 点![]() 在直线
在直线![]() 上,且
上,且![]() 关于直线
关于直线![]() 对称,
对称,
所以![]() ,且
,且![]() .
.
设![]() (
(![]() ),
),![]() 的中点为
的中点为![]() .
.
则![]() . 6分
. 6分
又![]() 在椭圆
在椭圆![]() 上,
上,
所以![]() .
.
所以![]() .
.
化简,得![]() .
.
所以![]() . 9分
. 9分
又因为![]() 的中点在直线
的中点在直线![]() 上,
上,
所以![]() .
.
所以![]() .
.
由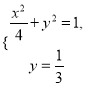 可得
可得![]() .
.
所以![]() ,或
,或![]() ,即
,即![]() ,或
,或![]() .
.
所以![]() 或
或![]() .. 12分
.. 12分
所以 对于![]() ,线段
,线段![]() 中点的纵坐标恒为
中点的纵坐标恒为![]() ,即线段
,即线段![]() 的中点总在直线
的中点总在直线![]() 上.
上.
13分

练习册系列答案
相关题目