题目内容
20.若函数f(x)=2cos2x-2acosx+a2-2a-1(0$≤x≤\frac{π}{2}$)的最小值为-2,求实数a的值并求此时f(x)的最大值.分析 化简可得f(x)=2(cosx-$\frac{a}{2}$)2+$\frac{{a}^{2}}{2}$-2a-1,结合0≤cosx≤1分类讨论由二次函数区间的最值可得.
解答 解:化简可得f(x)=2cos2x-2acosx+a2-2a-1
=2(cosx-$\frac{a}{2}$)2+$\frac{{a}^{2}}{2}$-2a-1
∵0$≤x≤\frac{π}{2}$,∴0≤cosx≤1,
当$\frac{a}{2}$<0即a<0时,函数f(x)在cosx∈[0,1]单调递增,
当cosx=0时函数f(x)取最小值a2-2a-1=2,解得a=-1,或a=3(舍去),
此时f(x)=2(cosx+$\frac{1}{2}$)2+$\frac{3}{2}$,当cosx=1时,函数取最大值6;
当0≤$\frac{a}{2}$≤1即0≤a≤2时,函数f(x)在cosx∈[0,$\frac{a}{2}$]单调递减,
在cosx∈[$\frac{a}{2}$,1]单调递增,当cosx=$\frac{a}{2}$时函数f(x)取最小值$\frac{{a}^{2}}{2}$-2a-1=2,
解得a=2±$\sqrt{10}$(舍去),不合题意;
当$\frac{a}{2}$>1即a>2时,函数f(x)在cosx∈[0,1]单调递减,
当cosx=1时函数f(x)取最小值a2-4a+1=2,解得a=2+$\sqrt{2}$,或a=2-$\sqrt{2}$(舍去),
此时当cosx=0时,函数取最大值2$\sqrt{2}$+1
综上可得当a=-1时,函数取最大值6,当a=2+$\sqrt{2}$时,函数取最大值2$\sqrt{2}$+1
点评 本题考查三角函数的最值,涉及二次函数区间的最值和分类讨论的思想,属中档题.

 阅读快车系列答案
阅读快车系列答案| A. | ±3 | B. | ±5 | C. | 3或5 | D. | ±3或±5 |
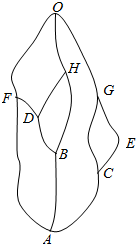 观日出,赏瀑布,或是重温老别墅里的民国往事和《庐山恋》的柔美爱情,庐山每天都吸引大量的国内外游客,从山脚的A点徒步攀登到山顶O处的主景区,沿途风景秀丽,令人流连忘返,下图是一张登山的地图,若游客在每一个岔路口选择哪一条路线上山是等可能的(假定游客始终沿上山路线前进,不往下走,例如从F不能向D点走)
观日出,赏瀑布,或是重温老别墅里的民国往事和《庐山恋》的柔美爱情,庐山每天都吸引大量的国内外游客,从山脚的A点徒步攀登到山顶O处的主景区,沿途风景秀丽,令人流连忘返,下图是一张登山的地图,若游客在每一个岔路口选择哪一条路线上山是等可能的(假定游客始终沿上山路线前进,不往下走,例如从F不能向D点走)