题目内容
已知双曲线C: (a>0,b>0)的离心率为
(a>0,b>0)的离心率为 ,且过点(4,3).
,且过点(4,3).
(1)求双曲线C的标准方程和焦点坐标;
(2)已知点P在双曲线C上,且∠F1PF2=90°,求点P到x轴的距离.
解:(1)∵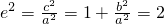 ∴a2=b2
∴a2=b2
∴双曲线C: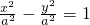 …(2分)
…(2分)
将点(4,3)代入得a2=b2=1…(4分)
∴双曲线C的标准方程为x2-y2=1,焦点坐标为F1(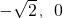 )和F2(
)和F2(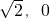 )…(6分)
)…(6分)
(2)由已知得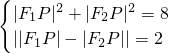 ∴|F1P|•|F2P|=2…(9分)
∴|F1P|•|F2P|=2…(9分)
所以点P到x轴的距离为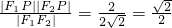 .…(12分)
.…(12分)
分析:(1)通过离心率与点在双曲线上,得到两个方程,求出a,b,即可求双曲线C的标准方程和焦点坐标;
(2)利用点P在双曲线C上,且∠F1PF2=90°,勾股定理与双曲线的定义列出方程,利用三角形的面积,求点P到x轴的距离.
点评:本题考查双曲线方程的求法,双曲线的简单性质,考查计算能力.
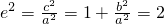 ∴a2=b2
∴a2=b2∴双曲线C:
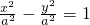 …(2分)
…(2分)将点(4,3)代入得a2=b2=1…(4分)
∴双曲线C的标准方程为x2-y2=1,焦点坐标为F1(
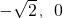 )和F2(
)和F2(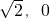 )…(6分)
)…(6分)(2)由已知得
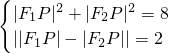 ∴|F1P|•|F2P|=2…(9分)
∴|F1P|•|F2P|=2…(9分)所以点P到x轴的距离为
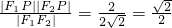 .…(12分)
.…(12分)分析:(1)通过离心率与点在双曲线上,得到两个方程,求出a,b,即可求双曲线C的标准方程和焦点坐标;
(2)利用点P在双曲线C上,且∠F1PF2=90°,勾股定理与双曲线的定义列出方程,利用三角形的面积,求点P到x轴的距离.
点评:本题考查双曲线方程的求法,双曲线的简单性质,考查计算能力.

练习册系列答案
相关题目


 (a>0,b>0)的左、右焦点分别为
(a>0,b>0)的左、右焦点分别为 、
、 ,离心率为3,直线y=2与C的两个交点间的距离为
,离心率为3,直线y=2与C的两个交点间的距离为 .
. ,证明:
,证明: 、
、 、
、 成等比数列.
成等比数列. (a>0)的一条渐近线与直线l:2x-y+1=0垂直,则实数a= .
(a>0)的一条渐近线与直线l:2x-y+1=0垂直,则实数a= .