题目内容
已知双曲线C:(1)求证:![]() ·
·![]() =
=![]() ·
·![]() ;
;
(2)若l与双曲线C的左、右两支分别交于点D、E,求双曲线C的离心率e的取值范围.
解析:(1)l:y=-![]() (x-c),
(x-c),
∴ P(
P(![]() ).
).
由|![]() |、|
|、|![]() |、|
|、|![]() |成等比数列得A(
|成等比数列得A(![]() ,0),
,0),
∴![]() =(0,-
=(0,-![]() ),
), ![]() =(
=(![]() ,
,![]() ),
), ![]() =(-
=(-![]() ,
,![]() ).
).
∴![]() ·
·![]() =
=![]() ·
·![]() .
.
(2)
∴b2x2-![]() (x-c)2=a2b2.
(x-c)2=a2b2.
即(b2-![]() )x2+2
)x2+2![]() cx-(
cx-(![]() +a2b2)=0,
+a2b2)=0,
∴Δ>0恒成立.
∴x1·x2= <0.
<0.
∴b4>a4,即b2>a2.
∴c2-a2>a2![]() e>
e>![]() .
.

练习册系列答案
相关题目








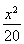




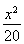

 =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 焦点到渐近线的距离为
焦点到渐近线的距离为

 与C有两个不同的交点,求实数k的取值范围;
与C有两个不同的交点,求实数k的取值范围; 求实数k的值.
求实数k的值.