题目内容
已知双曲线C: (a>0,b>0)的左、右焦点分别为
(a>0,b>0)的左、右焦点分别为 、
、 ,离心率为3,直线y=2与C的两个交点间的距离为
,离心率为3,直线y=2与C的两个交点间的距离为 .
.
(Ⅰ)求a,b;
(Ⅱ)设过 的直线l与C的左、右两支分别交于A、B两点,且
的直线l与C的左、右两支分别交于A、B两点,且 ,证明:
,证明: 、
、 、
、 成等比数列.
成等比数列.
【答案】
(Ⅰ) (Ⅱ)见解析
(Ⅱ)见解析
【解析】(Ⅰ)由题设知 ,即
,即 ,故
,故 .
.
所以C的方程为 .
.
将y=2代入上式,求得 .
.
由题设知, ,解得
,解得 .
.
所以 .
.
(Ⅱ)由(Ⅰ)知, ,
, ,C的方程为
,C的方程为 . ①
. ①
由题意可设 的方程为
的方程为 ,
, ,代入①并化简得
,代入①并化简得
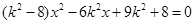 .
.
设 ,
, ,则
,则
 ,
, ,
, ,
, .
.
于是
 ,
,

由 得
得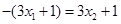 ,即
,即 .
.
故 ,解得
,解得 ,从而
,从而 .
.
由于 ,
,
 .
.
故 ,
,
 .
.
因而 ,所以
,所以 、
、 、
、 成等比数列.
成等比数列.
(1)利用待定系数法求解,利用已知条件建立含义 的等量关系,进而确定曲线方程;(2)利用直线与曲线联立方程组,借助韦达定理和弦长公式将
的等量关系,进而确定曲线方程;(2)利用直线与曲线联立方程组,借助韦达定理和弦长公式将 、
、 、
、 表示出来,然后借助
表示出来,然后借助 证明等比中项。
证明等比中项。
【考点定位】本题考查双曲线方程与直线与双曲线的位置关系,考查舍而不求的思想以及计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


 (a>0)的一条渐近线与直线l:2x-y+1=0垂直,则实数a= .
(a>0)的一条渐近线与直线l:2x-y+1=0垂直,则实数a= .