题目内容
已知双曲线C：
=1(a＞0,b＞0)，B是右顶点，F是右焦点，点A在x轴正半轴上，且|
|、|
|、|
|成等比数列，过F作双曲线C在第一、三象限的渐近线的垂线l，垂足为P.
（1）求证：
·
=
·
；
（2）若l与双曲线C的左、右两支分别相交于点D、E，求双曲线离心率e的取值范围.
(1)证明：欲证
·=·,只需证·（-）=0，即证·（+
）=
·
=0，即证
⊥
.∵|
|2=|
||
|，∴a2=|
|c.
∴|
|=
.∴A(
,0).
∵PF⊥OP,∴lFP:y=-
(x-c).
由
解得
.
∴
⊥
.
∴原命题得证.
(2)解析：若l与双曲线两支各有一交点，则由渐近线性质得kFP＞-
,即-
＞-
.∴a2＜b2=c2-a2.
∴2a2＜c2.∴e=
＞
.
练习册系列答案
高中必刷题系列答案
相关题目
-
=1（0＜
＜1）的右焦点为B，过点B作直线交双曲线C的右支于M、N两点，试确定
·
=0，其中点O为坐标原点.
-
=1的焦距为10 ，点P （2,1）在C 的渐近线上，则C的方程为
-
=1 B.
-
=1 C.
-
=1
=1（a＞0，b＞0）的离心率为
，右准线方程为x=
-
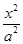=1的焦距为10 ，点P （2,1）在C 的渐近线上，则C的方程为(
)
-
=1
B. 
-
=1 C. 
-
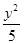=1
-
=1的焦距为10 ，点P （2,1）在C 的渐近线上，则C的方程为
-
=1 B、
-
=1
C、
-
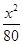=1[w~#