题目内容
11.已知f(x)与g(x)分别是定义在R上的奇函数与偶函数,若f(x)+g(x)=x2-x+2.则f(1)等于( )| A. | $-\frac{1}{2}$ | B. | -1 | C. | 3 | D. | $\frac{3}{2}$ |
分析 由题意,在f(x)+g(x)=x2-x+2中,令x=1和-1可得:f(1)+g(1)=2①,f(-1)+g(-1)=4,结合函数的奇偶性可得:-f(1)+g(1)=4③,联合①、③可得答案.
解答 解:根据题意,在f(x)+g(x)=x2-x+2中,令x=1可得,f(1)+g(1)=2,①
令x=-1可得,f(-1)+g(-1)=4,②
而f(x)与g(x)分别是定义在R上的奇函数与偶函数,
则f(-1)=-f(1),g(-1)=g(1),
则②可以变形为:-f(1)+g(1)=4,③
①-③可得:2f(1)=-2,
则f(1)=-1;
故选:B.
点评 本题考查函数的奇偶性性质的运用,以及利用函数的这一性质求函数值,一般结合奇偶性利用赋值法分析计算.

练习册系列答案
相关题目
2.圆的一条直径为x=2(-2≤y≤0),则此圆的方程是( )
| A. | (x-2)2+(y-1)2=1 | B. | (x-2)2+(y+1)2=1 | C. | (x+2)2+(y-1)2=1 | D. | (x+2)2+(y+1)2=1 |
3.函数y=$\frac{2x}{lnx}$的图象大致为( )
| A. |  | B. | 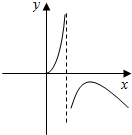 | C. | 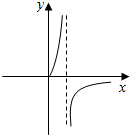 | D. | 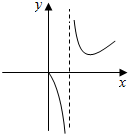 |