题目内容
三棱锥P-ABC的高PO=8,AC=BC=3,∠ACB=30°,M、N分别在BC和PO上,且CM=x,PN=3CM,试问下面的四个图象中,那个图象大致描绘了三棱锥N-AMC的体积V与x的变化关系(x∈[0,3])( )
A.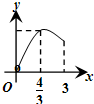 | B.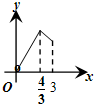 | C.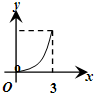 | D.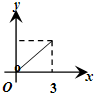 |
底面三角形ABC的边AC=3,CM=x,∠ACB=30°,
∴△ACM的面积为:
x•3•sin30°=
x
又∵三棱锥N-AMC的高NO=PO-PN=8-3x
所以三棱锥N-AMC的体积V=
(8-3x)
x=-
x2+2x
当x=
时取得最大值,开口向下的二次函数,
故选A.
∴△ACM的面积为:
| 1 |
| 2 |
| 3 |
| 4 |
又∵三棱锥N-AMC的高NO=PO-PN=8-3x
所以三棱锥N-AMC的体积V=
| 1 |
| 3 |
| 3 |
| 4 |
| 3 |
| 4 |
当x=
| 4 |
| 3 |
故选A.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目